(本小题满分12分)
某班主任统计本班50名学生放学回家后学习时间的数据,用条形图表示(如图)。
(1)求该班学生每天在家学习时间的平均值;
(2)该班主任用分层抽样方法(按学习时间分五层)选出10个学生谈话,求在学习时间为1个小时的学生中选出的人数;
(3)假设学生每天在家学习时间为18时至23时,已知甲每天连续学习2小时,乙每天连续学习3小时,求19时至20时甲、乙都在学习的概率.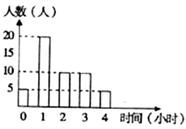
已知函数
(1)试判断函数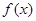 的单调性;
的单调性;
(2)设 ,求
,求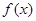 在
在 上的最大值;
上的最大值;
(3)试证明:对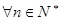 ,不等式
,不等式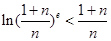 .
.
如图,在四棱锥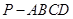 中,底面
中,底面 为直角梯形,且
为直角梯形,且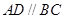 ,
, ,侧面
,侧面 底面
底面 . 若
. 若 .
.
(1)求证: 平面
平面 ;
;
(2)侧棱 上是否存在点
上是否存在点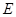 ,使得
,使得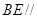 平面
平面 ?若存在,指出点
?若存在,指出点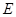 的位置并证明,若不存在,请说明理由;
的位置并证明,若不存在,请说明理由;
(3)求二面角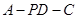 的余弦值.
的余弦值.
在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,记ξ=|x-2|+|y-x|.
(1)求随机变量ξ的最大值,并求事件“ξ取得最大值”的概率;
(2)求随机变量ξ的分布列.
已知曲线 :
: (
( 为参数),
为参数), :
: (
( 为参数).
为参数).
(1)化 ,
, 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若 上的点
上的点 对应的参数为
对应的参数为 ,
, 为
为 上的动点,求
上的动点,求 中点
中点 到直线
到直线 :
: (
( 为参数)距离的最小值.
为参数)距离的最小值.
设f(x)=2x3+ax2+bx+1的导数为f′(x),若函数y=f′(x)的图象关于直线x=- 对称,且f′(1)=0.
对称,且f′(1)=0.
(1)求实数a,b的值;
(2)求函数f(x)的极值.