某校从参加高一年级期中考试的学生中随机抽取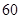 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段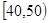 ,
,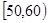 …
…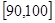 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: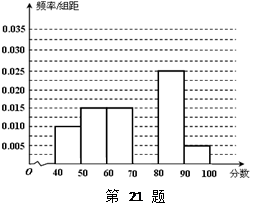
(Ⅰ)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)用分层抽样的方法在分数段为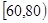 的学生中抽取一个容量为
的学生中抽取一个容量为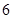 的样本,
的样本,
将该样本看成一个总体,从中任取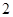 人,求至多有
人,求至多有 人在分数段
人在分数段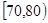 的概率.
的概率.
(本小题10分)
如图,半径为2的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的体积。(其中∠BAC=30°)
(本小题满分12分)
已知函数f(x)=lnx- ,其中a为常数,且a>0.
,其中a为常数,且a>0.
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直,求函数f(x)的单调递减区间;
(2)若函数f(x)在区间[1,3]上的最小值为 ,求a的值.
,求a的值.
(本小题满分12分)时下网校教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量y(单位:千套)与销售价格x(单位:元/套)满足的关系式y=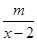 +4(x-6)2,其中2<x<6,m为常数.已知销售价格为4元/套时,每日可售出套题21千套.
+4(x-6)2,其中2<x<6,m为常数.已知销售价格为4元/套时,每日可售出套题21千套.
(1)求m的值;
(2)假设网校的员工工资、办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格x的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
(本小题满分12分)已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,3]上有最大值4和最小值1.设f(x)=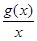 .
.
(1)求a、b的值;
(2)若不等式f(2x)-k·2x≥0在x∈[-1,1]上有解,求实数k的取值范围.
(本小题满分12分)如图是函数f(x)=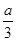 x3-2x2+3a2x的导函数y=
x3-2x2+3a2x的导函数y=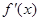 的简图,它与x轴的交点是(1,0)和(3,0)
的简图,它与x轴的交点是(1,0)和(3,0)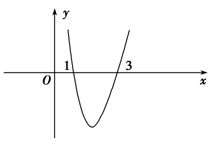
(1)求函数f(x)的极小值点和单调递减区间;
(2)求实数a的值.