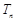如图,四棱锥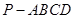 的底面
的底面 是矩形,
是矩形,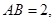
 ,且侧面
,且侧面 是正三角形,平面
是正三角形,平面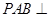 平面
平面 ,
,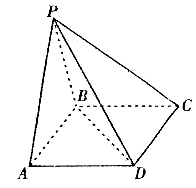
(Ⅰ)求证: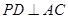 ;
;
(Ⅱ)在棱 上是否存在一点
上是否存在一点 ,使得二面角
,使得二面角 的大小为45°.若存在,试求
的大小为45°.若存在,试求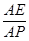 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知数列 的前
的前 项和为
项和为 ,
,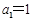 ,
,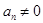 ,
,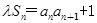 ,其中
,其中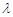 为常数.
为常数.
(1)证明:数列 是等差数列;
是等差数列;
(2)是否存在实数λ,使得 为等差数列?并说明理由;
为等差数列?并说明理由;
(3)若 为等差数列,令
为等差数列,令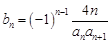 ,求数列
,求数列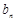 的前
的前 项和
项和 .
.
在平面直角坐标系中,圆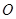 :
: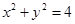 与
与 轴的正半轴交于点
轴的正半轴交于点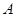 ,以
,以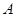 为圆心的圆
为圆心的圆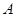 :
: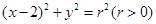 与圆
与圆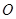 交于
交于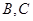 两点.
两点.
(1)若直线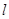 与圆
与圆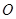 切于第一象限,且与坐标轴交于
切于第一象限,且与坐标轴交于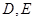 ,当线段
,当线段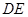 长最小时,求直线
长最小时,求直线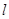 的方程;
的方程;
(2)设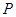 是圆
是圆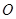 上异于
上异于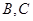 的任意一点,直线
的任意一点,直线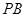 、
、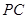 分别与
分别与 轴交于点
轴交于点 和
和 ,问
,问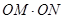 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
为响应国家扩大内需的政策,某厂家拟在2016年举行某一产品的促销活动,经调查测算,该产品的年销量(即该厂的年产量)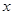 万件与年促销费用
万件与年促销费用
 万元满足
万元满足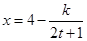 (k为常数).如果不搞促销活动,则该产品的年销量只能是1万件.已知2016年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均生产投入成本的1.5倍(生产投入成本包括生产固定投入和生产再投入两部分).
(k为常数).如果不搞促销活动,则该产品的年销量只能是1万件.已知2016年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均生产投入成本的1.5倍(生产投入成本包括生产固定投入和生产再投入两部分).
(1)求常数k,并将该厂家2016年该产品的利润y万元表示为年促销费用t万元的函数;
(2)该厂家2016年的年促销费用投入多少万元时,厂家利润最大?
在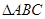 中,
中,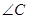 的平分线所在直线
的平分线所在直线 的方程为
的方程为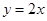 ,若点
,若点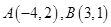 .
.
(1)求点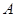 关于直线
关于直线 的对称点
的对称点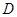 的坐标;
的坐标;
(2)求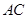 边上的高所在的直线方程;
边上的高所在的直线方程;
(3)求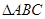 得面积.
得面积.
等比数列 中,
中,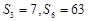 .
.
(1)求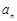 ;
;
(2)记数列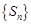 的前
的前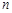 项和为
项和为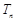 ,求
,求