已知椭圆方程为 斜率为
斜率为 的直线过椭圆的上焦点且与椭圆相交于P,Q两点,线段PQ的垂直平分线与y轴交于点M(0,m)。
的直线过椭圆的上焦点且与椭圆相交于P,Q两点,线段PQ的垂直平分线与y轴交于点M(0,m)。
(1)求m的取值范围;
(2)求△OPQ面积的取值范围。
(本小题满分12分)已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.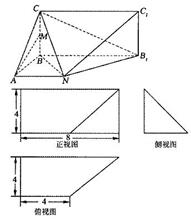
(Ⅰ)若M为CB中点,证明: ;
;
(Ⅱ)求这个几何体的体积.
(本小题满分12分)某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组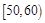 ,第二组
,第二组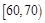 ,…,第五组
,…,第五组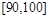 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图.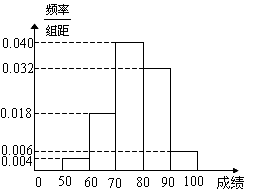
(Ⅰ)若成绩大于或等于60且小于80,认为合格,求该班在这次数学测试中成绩合格的人数;
(Ⅱ)从测试成绩在 内的所有学生中随机抽取两名同学,设其测试成绩分别为m、n,求事件“
内的所有学生中随机抽取两名同学,设其测试成绩分别为m、n,求事件“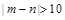 ”概率.
”概率.
(本小题12分)等比数列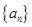 的各项均为正数,且
的各项均为正数,且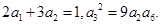
(Ⅰ)求数列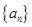 的通项公式;
的通项公式;
(Ⅱ)设 求数列
求数列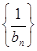 的前n项和.
的前n项和.
(本小题满分10分)在锐角
(Ⅰ)求角C;
(Ⅱ)设 的面积.[
的面积.[
已知函数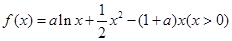 ,其中
,其中 为实数.
为实数.
(1)求函数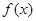 的单调区间;
的单调区间;
(2)若函数 对定义域内的任意
对定义域内的任意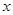 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(3)证明,对于任意的正整数 ,不等式
,不等式 恒成立.
恒成立.