2011年3月,日东发生了9。0级地震,地震引发了海啸及核泄漏某国际组织用分层抽样的方法从心理专家、核专家、地质专家三类专家中抽取若干人组成研究团队赴日东工作,有关数据见表1:(单位:人)
核专家为了检测当地动物受核辐射后对身体健康的影响,随机选取了110只羊进行了检测,并将有关数据整理为不完整的2×2列联表(表2)
附:临界值表K2=
| K0 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10. 828 |
| P(K2≥K0) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
(1)求研究小组的总人数 (2)写出表中的A、B、C、D、E值,并判断有多大把握认为羊受到高度辐射与身体不健康有关。
如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点. 
(1)若直线PQ过定点 ,求点A的坐标;
,求点A的坐标;
(2)对于第(1)问的点A,三角形APQ能否为等腰直角三角形?若能,试确定三角形APD的个数;若不能,说明理由.
如图,在直角梯形ABCP中, ,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP
,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP 平面EFG;(2)当二面角G-EF-D的大小为
平面EFG;(2)当二面角G-EF-D的大小为 时,求FG与平面PBC所成角的余弦值.
时,求FG与平面PBC所成角的余弦值.
某市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的被淘汰.若有500人参加测试,学生成绩的频率分布直方图如图.
(1)求获得参赛资格的人数;
(2)根据频率直方图,估算这500名学生测试的平均成绩;
(3)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛.已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响.已知他连续两次答错的概率为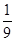 ,求甲在初赛中答题个数
,求甲在初赛中答题个数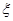 的分布列及数学期望
的分布列及数学期望 .
.
已知函数
(1)求函数 的最大值,并写出
的最大值,并写出 取最大值
取最大值 时的取值集合;
时的取值集合;
(2)在 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 求
求 的最小值.
的最小值.
已知函数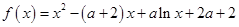 (其中
(其中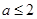 ).
).
(1)求函数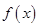 的单调区间;
的单调区间;
(2)若函数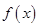 在
在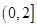 上有且只有一个零点,求实数
上有且只有一个零点,求实数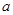 的取值范围.
的取值范围.