在我县举行的“建县2700年”唱红歌比赛活动中,共有40支参赛队。有关部门对本次活动的获奖情况进行了统计,并根据收集的数据绘制了图6、图7两幅不完整的统计图,请你根据图中提供的信息解答下面的问题:
1、获一、二、三等奖各有多少参赛队?
2、在答题卷上将统计图图6补充完整。
3、计算统计图图7中“没获将”部分所对应的圆心角的度数
4、求本次活动的获奖概率。
图6
已知集合A={x|x2-2x-3≤0},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1) 当m=2时,求A B;
B;
(2) 若A∩B=[1,3],求实数m的值;
(3) 若A⊆∁RB,求实数m的取值范围.
设函数f(x)= 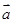 ×
×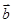 ,其中向量
,其中向量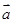 ="(2cosx,1),"
="(2cosx,1)," 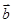 =(cosx,
=(cosx, sin2x+m).
sin2x+m).
(1)求函数f(x)的最小正周期和f(x)在[0, p]上的单调递增区间;
(2)当xÎ[0, ]时,ô f(x)ô <4恒成立,求实数m的取值范围.
]时,ô f(x)ô <4恒成立,求实数m的取值范围.
已知向量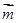 =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量 =(2,0)所成角为
=(2,0)所成角为 ,其中A、B、C是△ABC的内角。
,其中A、B、C是△ABC的内角。
(1)求角B的大小;
(2)求sinA+sinC的取值范围。
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)现从乙班这10名同学中随机抽取两名身高不低于173 cm的同学,求身高为176 cm的同学被抽中的概率.
已知函数f(x)是定义在R上的奇函数,并且当x∈(0,+∞)时,f(x)=2x.
(1)求f(log2 )的值;
)的值;
(2)求f(x)的解析式.