在平面直角坐标平面内,已知点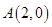 ,
,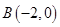 ,
,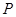 是平面内一动点,直线
是平面内一动点,直线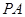 、
、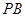 斜率之积为
斜率之积为 .
.
(1)求动点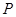 的轨迹
的轨迹 的方程;
的方程;
(2)过点 作直线
作直线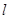 与轨迹
与轨迹 交于
交于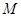 、
、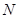 两点,
两点,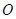 为坐标原点,求△
为坐标原点,求△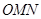 面积取最大值时,直线
面积取最大值时,直线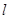 的方程.
的方程.
已知椭圆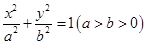 的离心率为
的离心率为 ,点
,点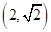 在
在 上.
上.
(1)求 的标准方程;
的标准方程;
(2)设直线 过点
过点 ,当
,当 绕点
绕点 旋转的过程中,与椭圆
旋转的过程中,与椭圆 有两个交点
有两个交点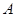 ,
,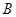 ,求线段
,求线段 的中点
的中点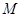 的轨迹方程.
的轨迹方程.
如图,矩形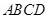 的两条对角线相交于点
的两条对角线相交于点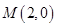 ,
,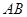 边所在直线的方程为
边所在直线的方程为 ,点
,点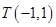 在
在 边所在直线上.
边所在直线上.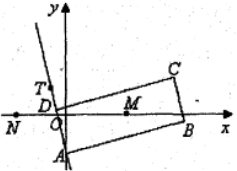
(1)求 所在直线的方程;
所在直线的方程;
(2)求矩形 外接圆的方程.
外接圆的方程.
设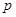 :实数
:实数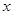 满足
满足 ,其中
,其中 ,命题
,命题 :实数
:实数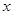 满足
满足
(1)若 ,且
,且 为真,求实数
为真,求实数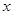 的取值范围;
的取值范围;
(2)若 是
是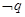 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
对于函数 ,如果存在实数
,如果存在实数 、
、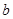 使得
使得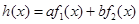 ,那么称
,那么称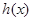 为
为 的生成函数.
的生成函数.
(1)下面给出两组函数,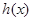 是否为
是否为 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组: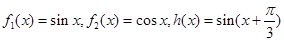 ;
;
第二组: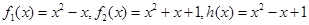 .
.
(2)设 ,
,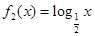 ,
, ,生成函数
,生成函数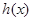 ,若不等式
,若不等式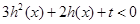 在
在 上有解,求实数t的取值范围.
上有解,求实数t的取值范围.