直四棱柱 的底面
的底面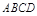 是菱形,
是菱形, ,其侧面展开图是边长为
,其侧面展开图是边长为 的正方形.
的正方形. 、
、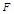 分别是侧棱
分别是侧棱 、
、 上的动点,
上的动点, .
.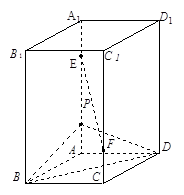
(Ⅰ)证明: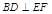 ;
;
(Ⅱ) 在棱
在棱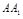 上,且
上,且 ,若
,若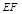 ∥平面
∥平面 ,求
,求 .
.
辽宁号航母纪念章从2012年10月5日起开始上市.通过市场调查,得到该纪念章每1枚的市场价 (单位:元)与上市时间
(单位:元)与上市时间 (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 天 天 |
4 |
10 |
36 |
市场价 元 元 |
90 |
51 |
90 |
(1)根据上表数据结合散点图,从下列函数中选取一个恰当的函数描述辽宁号航母纪念章的市场价 与上市时间
与上市时间 的变化关系并说明理由:①
的变化关系并说明理由:① ;②
;②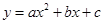 ;③
;③ .
.
(2)利用你选取的函数,求辽宁号航母纪念章市场价最低时的上市天数及最低的价格.
已知函数 .
.
(1)求 的最小正周期;
的最小正周期;
(2)若 ,求
,求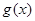 在区间
在区间 上的值域.
上的值域.
已知 ,其中
,其中 .
.
(1)求 的值;
的值;
(2)求角 的值.
的值.
已知集合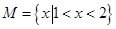 ,集合
,集合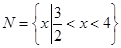 .
.
(1)求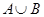 ;
;
(2)设集合 ,若
,若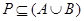 ,求实数
,求实数 的取值范围.
的取值范围.
如图,在体积为 的圆锥
的圆锥 中,已知
中,已知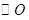 的直径
的直径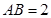 ,
,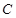 是
是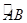 的中点,
的中点,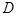 是弦
是弦 的中点.
的中点.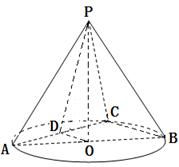
(1)指出二面角 的平面角,并求出它的大小;
的平面角,并求出它的大小;
(2)求异面直线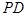 与
与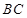 所成的角的正切值.
所成的角的正切值.