(本小题10分)选修4—5:不等式选讲
已知函数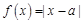
(1)若不等式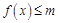 的解集为
的解集为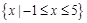 ,求实数
,求实数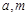 的值;
的值;
(2)当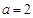 时,解关于
时,解关于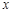 的不等式
的不等式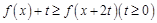 .
.
数列 的前n项和为
的前n项和为 ,
, ,且对任意的
,且对任意的 均满足
均满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,
, ,
, (
( ),求数列
),求数列 的前
的前 项和
项和 .
.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB= 60°,FC⊥平面ABCD,AE⊥BD,CB=" CD=" CF.
(1)求证:BD⊥平面AED;
(2)求二面角F—BD—C的正切值.
已知向量
(1)当 时,求
时,求 的值;
的值;
(2)求函数 在
在 上的值域.
上的值域.
某网站针对“2014年法定节假日调休安排”展开的问卷调查,提出了A、B、C三种放假方案,调查结果如下:
| 支持A方案 |
支持B方案 |
支持C方案 |
|
| 35岁以下 |
200 |
400 |
800 |
| 35岁以上(含35岁) |
100 |
100 |
400 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持A方案”的人中抽取了6人,求n的值;
(2)在“支持B方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率.
设函数 在
在 上的最大值为
上的最大值为 (
( ).
).
(1)求数列 的通项公式;
的通项公式;
(2)求证:对任何正整数n (n≥2),都有 成立;
成立;
(3)设数列 的前n项和为Sn,求证:对任意正整数n,都有
的前n项和为Sn,求证:对任意正整数n,都有 成立.
成立.