利用余弦函数y=cosx的图像,比较x=0,x=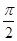 附近的平均变化率的大小。
附近的平均变化率的大小。
在 中,
中,
(1)求 的值;
的值;
(2)求 的面积.
的面积.
设函数 (1)当
(1)当 时,求不等式
时,求不等式 的解集;(2)若
的解集;(2)若 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围.
在直角坐标系中,以原点为极点,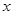 轴的正半轴为极轴建立极坐标系,两种坐标系取相同单位长度.已知曲线
轴的正半轴为极轴建立极坐标系,两种坐标系取相同单位长度.已知曲线 过点
过点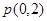 的直线
的直线 的参数方程为
的参数方程为 (t为参数). (1)求曲线C与直线
(t为参数). (1)求曲线C与直线 的普通方程;(2)设曲线C经过伸缩变换
的普通方程;(2)设曲线C经过伸缩变换 得到曲线
得到曲线 ,若直线
,若直线 与曲线
与曲线 相切,求实数
相切,求实数 的值.
的值.
如图,在锐角三角形ABC中,D 为C在AB上的射影,E 为D在BC上的射影,F为DE上一点,且满足

(1)证明: (2)若AD=2,CD=3.DB=4,求
(2)若AD=2,CD=3.DB=4,求 的值.
的值.
已知函数 图像上一点
图像上一点 处的切线方程为
处的切线方程为 (1)求
(1)求 的值;(2)若方程
的值;(2)若方程 在区间
在区间 内有两个不等实根,求
内有两个不等实根,求 的取值范围;(3)令
的取值范围;(3)令 如果
如果 的图像与
的图像与 轴交于
轴交于 两点,
两点, 的中点为
的中点为 ,求证:
,求证: