计算：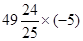
；
如图，在边长为1的5×5的正方形网格上有两个三角形，它们顶点都在格点上．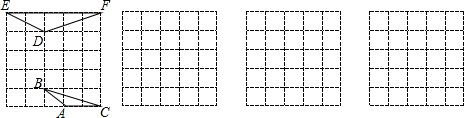
（1）△ABC与△DEF是否相似？请说明理由；
（2）还能在网格上画出与△ABC相似的三角形吗？还能画出几种大小不同的？试着在备用图上画出来（三个顶点都在格点上哟）．
如图，已知抛物线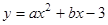
的对称轴为直线
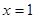，交
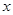轴于A、B两点，交
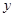轴于C点，其中B点的坐标为（3,0）。
（1）直接写出A点的坐标；
（2）求二次函数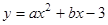的解析式。
如图，D是△ABC的边AC上的一点，连接BD，已知∠ABD=∠C，AB=6，AD=4，求线段CD的长．
已知二次函数y=-2x2+4x+6
（1）求函数图象的顶点坐标及对称轴
（2）求此抛物线与x轴的交点坐标．
已知，如图，△ABC中．AD⊥BC于D，AC=10，BC=21，△ABC面积为84，求sinBcosC+cosBsinC的值．