(本题14分)设 是公比大于1的等比数列,
是公比大于1的等比数列, 为数列
为数列 的前
的前 项和。
项和。
已知 ,且
,且 构成等差数列.
构成等差数列.
(1)求 数列的通项公式.
数列的通项公式.
(2)令 ,求数列
,求数列 的前
的前 项和
项和 .
.
(3) ,求数列
,求数列 的前
的前 项和
项和 .
.
已知等比数列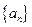 的首项为
的首项为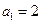 ,公比为
,公比为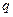 (
(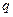 为正整数),且满足
为正整数),且满足 是
是 与
与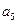 的等差中项;数列
的等差中项;数列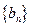 满足
满足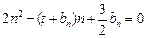 (
(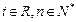 ).
).
(1)求数列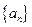 的通项公式;
的通项公式;
(2)试确定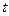 的值,使得数列
的值,使得数列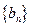 为等差数列;
为等差数列;
(3)当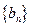 为等差数列时,对任意正整数
为等差数列时,对任意正整数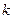 ,在
,在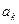 与
与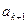 之间插入2共
之间插入2共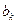 个,得到一个新数列
个,得到一个新数列 .设
.设 是数列
是数列 的前
的前 项和,试求满足
项和,试求满足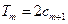 的所有正整数
的所有正整数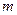 的值。
的值。
在直角坐标系xOy中,椭圆C1: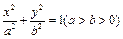 的左、右焦点分别为F1、F2,其中右焦点F2也是拋物线C2:y2 = 4x的焦点,点M为C1与C2在第一象限的交点,且|MF2| =
的左、右焦点分别为F1、F2,其中右焦点F2也是拋物线C2:y2 = 4x的焦点,点M为C1与C2在第一象限的交点,且|MF2| = 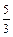 .
.
(1)求椭圆C1的方程;
(2)设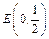 ,是否存在斜率为k (k≠0)的直线l与椭圆C1交于A、B两点,且|AE| = |BE|?若存在,求k的取值范围;若不存在,请说明理由.
,是否存在斜率为k (k≠0)的直线l与椭圆C1交于A、B两点,且|AE| = |BE|?若存在,求k的取值范围;若不存在,请说明理由.
某电视生产企业有A、B两种型号的电视机参加家电下乡活动,若企业投放A、B两种型号电视机的价值分别为a、b万元,则农民购买电视机获得的补贴分别为 万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
(1)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(2)求当投放B型电视机的金额为多少万元时,农民得到的总补贴最大?
如图,在等腰梯形ABCD中,AB∥DC,AB = 4,CD = 2,等腰梯形的高为3,O为AB中点,PO⊥平面ABCD,垂足为O,PO = 2,EA∥PO.
(1)求证:BD⊥平面EAC;
(2)求二面角E—AC—P的平面角的余弦值.
“上海世博会”将于2010年5月1日至10月31日在上海举行。世博会“中国馆·贵宾厅”作为接待中外贵宾的重要场所,其中陈列的艺术品是体现兼容并蓄、海纳百川的重要文化载体,为此,上海世博会事物协调局将举办“中国2010年上海世博会‘中国馆·贵宾厅’艺术品方案征集”活动.某地美术馆从馆藏的中国画、书法、油画、陶艺作品中各选一件代表作参与应征,假设这四件代表作中中国画、书法、油画入选“中国馆·贵宾厅”的概率均为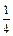 ,陶艺入选“中国馆·贵宾厅”的概率为
,陶艺入选“中国馆·贵宾厅”的概率为 .假定这四件作品是否入选相互没有影响.
.假定这四件作品是否入选相互没有影响.
(1)求该地美术馆选送的四件代表作中恰有一件作品入选“中国馆·贵宾厅”的概率;
(2)设该地美术馆选送的四件代表作中入选“中国馆·贵宾厅”的作品件数为随机变量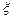 ,求
,求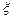 的数学期望.
的数学期望.