(本大题12分)
已知函数 .
.
(Ⅰ)求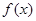 的最小正周期,并求其单调递增区间;
的最小正周期,并求其单调递增区间;
(Ⅱ)当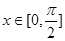 时,求
时,求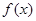 的值域.
的值域.
已知函数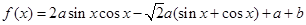 的定义域为
的定义域为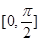 ,值域为
,值域为 .
.
(1)求实数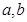 的值;
的值;
(2)数列 中,有
中,有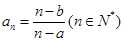 . 则该数列有最大项、最小项吗?若有,求出数列的最大项、最小项;若没有,请说明理由.
. 则该数列有最大项、最小项吗?若有,求出数列的最大项、最小项;若没有,请说明理由.
若数列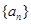 的前n项和为
的前n项和为 ,且有
,且有 ,
,
(1)求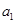 的值;
的值;
(2)求证: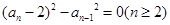 ;
;
(3)求出所有满足条件的数列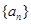 的通项公式;
的通项公式;
下列关于星星的图案构成一个数列 ,
,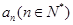 对应图中星星的个数.
对应图中星星的个数.
(1)写出 的值及数列
的值及数列 的通项公式;
的通项公式;
(2)求出数列 的前n项和
的前n项和 ;
;
(3)若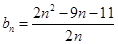 ,对于(2)中的
,对于(2)中的 ,有
,有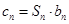 ,求数列
,求数列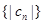 的前n项和
的前n项和 ;
;
已知函数 ,
,
(1)求函数f (x)的最小值和最小正周期;
(2)设△ABC的内角A、B、C的对应边分别为 、b、c,且
、b、c,且 ,若向量
,若向量 共线,求
共线,求 、b的值;
、b的值;