(本小题满分12分)如图所示是某水产养殖场的养殖大网箱的平面-优题课

题文

(本小题满分12分)如图所示是某水产养殖场的养殖大网箱的平面图，四周的实线为网衣，为避免混养，用筛网(图中虚线)把大网箱隔成大小一样的小网箱．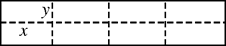

(1)若大网箱的面积为108平方米，每个小网箱的长x，宽y设计为多少米时，才能使围成的网箱中筛网总长度最小；
(2)若大网箱的面积为160平方米，网衣的造价为112元/米，筛网的造价为96元/米，且大网箱的长与宽都不超过15米，则小网箱的长、宽为多少米时，可使总造价最低？

科目数学题型解答题难度较易

登录免费查看答案和解析

相关试题

在平面直角坐标系中，以坐标原点 $O$ 为极点， $x$ 轴的正半轴为极轴建立极坐标系。已知直线 $l$ 上两点 $M, N$ 的极坐标分别为（2,0）( $\frac{2 \sqrt{3}}{3}, \frac{π}{2}$ ),圆 $C$ 的参数方程 $\{\begin{cases} x = 2 + 2 \cos θ \\ y = - \sqrt{3} + 2 \sin θ \end{cases} (θ 为参数)$

（1）设 $P$ 为线段 $M N$ 的中点，求直线 $O P$ 的平面直角坐标方程

（2）判断直线 $l$ 与圆 $C$ 的位置关系

已知函数 $f (x) = m - | x - 2 |$ ， $m \in R$ ，且 $f (x + 2) \geq 0$ 的解集为 $[- 1, 1]$ .
（Ⅰ）求 $m$ 的值；
（Ⅱ）若 $a, b, c \in R$ ，且 $\frac{1}{a} + \frac{1}{2 b} + \frac{1}{3 c} = m$ ，求证： $a + 2 b + 3 c \geq 9$ .

设曲线 $2 x^{2} + 2 x y + y^{2} = 1$ 在矩阵 $A = (\begin{matrix} a & 0 \\ b & 1 \end{matrix}) (a > 0)$ 对应的变换作用下得到的曲线为 $x^{2} + y^{2} = 1$ .

（Ⅰ）求实数 $a, b$ 的值
（Ⅱ）求 $A^{2}$ 的逆矩阵

已知函数 $f (x) = e^{x} + a x^{2} - e x, a \in R$ .
（Ⅰ）若曲线 $y = f (x)$ 在点 $(1, f (1))$ 处的切线平行于 $x$ 轴，求函数 $f (x)$ 的单调区间；
（Ⅱ）试确定 $a$ 的取值范围，使得曲线 $y = f (x)$ 上存在唯一的点 $P$ ，曲线在该点处的切线与曲线只有一个公共点 $P$ .

如图，椭圆 $E$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左焦点为 $F_{1}$ ，右焦点为 $F_{2}$ ，离心率 $e = \frac{1}{2}$ 。过 $F_{1}$ 的直线交椭圆于 $A, B$ 两点，且 $△ A B F_{2}$ 的周长为8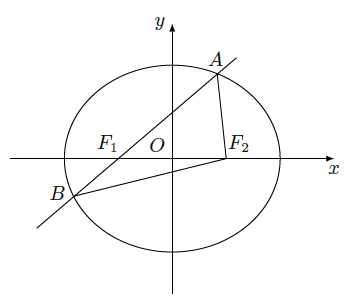

（Ⅰ）求椭圆 $E$ 的方程。
（Ⅱ）设动直线 $l$ ： $y = k x + m$ 与椭圆 $E$ 有且只有一个公共点 $P$ ，且与直线 $x = 4$ 相较于点 $Q$ 。试探究：在坐标平面内是否存在定点 $M$ ，使得以 $P Q$ 为直径的圆恒过点 $M$ ？若存在，求出点 $M$ 的坐标；若不存在，说明理由

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号