(本小题满分12分) 已知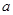
为实数，
，
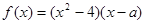（Ⅰ）若a=2，求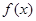
的单调递增区间；
（Ⅱ）若
，求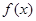在[－2，2] 上的最大值和最小值。
已知：△ABC中，顶点A（2，2），边AB上的中线CD所在直线的方程是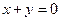
，边AC上的高BE所在直线的方程是
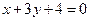.（1）求点B、C的坐标；（2）求△ABC的外接圆的方程.
已知直三棱柱ABC—A1B1C1的侧棱长与底面三角形的各边长都等于a，D为BC的中点，（1）求证：A1B∥平面AC1D．
（2）若点M为CC1中点，求证：平面A1B1M⊥平面ADC1
已知直线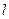
过点P（2，3），并与
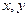轴正半轴交于A,B二点。
（1）当
AOB面积为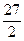
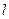时，求直线的方程。
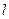（2）求AOB面积的最小值，并写出这时的直线的方程。
已知直线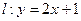
求：
（1）直线关于点M（3，2）的对称的直线方程。
（2）直线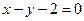
关于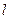
的对称的直线方程。
在四棱锥P-ABCD中，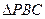
为正三角形，AB
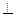平面PBC，AB//CD，AB=
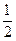DC，E为PD中点。（1）求证：AE//平面PBC
（2）求证：AE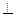平面PDC