已知 ,
,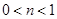 ;命题
;命题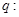 关于
关于 的方程
的方程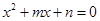 有两个小于1的正根 .试分析
有两个小于1的正根 .试分析 是
是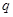 的什么条件 .
的什么条件 .
分别写出下列命题的逆命题,否命题,逆否命题,并判断其真假.
(1)矩形的对角线相等且互相平分;
(2)正偶数不是质数.
若F1、F2分别为双曲线 -=1下、上焦点,O为坐标原点,P在双曲线的下支上,点M在上准线上,且满足: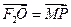 ,
,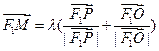
(1)求此双曲线的离心率;
(2)若此双曲线过N(,2),求此双曲线的方程
(3)若过N(,2)的双曲线的虚轴端点分别B1,B2(B2在x轴正半轴上),点A、B在双曲线上,且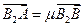 ,求
,求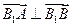 时,直线AB的方程.
时,直线AB的方程.
如图,正四棱锥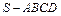 的高
的高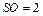 ,底边长
,底边长 .求异面直线
.求异面直线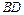 和
和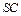 之间的距离.
之间的距离.
如图,正方形 与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,
与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,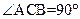 , F、G分别是线段AE、BC的中点.求
, F、G分别是线段AE、BC的中点.求 与
与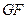 所成的角的大小.
所成的角的大小.
椭圆的中心是原点O,它的短轴长为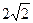 ,相应于焦点F(c,0)(
,相应于焦点F(c,0)(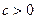 )的准线
)的准线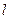 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
(Ⅰ)求椭圆的方程及离心率;
(Ⅱ)若 ,求直线PQ的方程;
,求直线PQ的方程;
(Ⅲ)设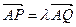 (
(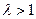 ),过点P且平行于准线
),过点P且平行于准线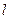 的直线与椭圆相交于另一点M,证明:
的直线与椭圆相交于另一点M,证明: .
.