(本小题满分12分)
已知焦点在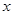
轴上的双曲线C的两条渐近线过坐标原点，且两条渐近线与以点
为圆心，1为半径的圆相切，又知C的一个焦点与A关于直线
对称．
（1）求双曲线C的方程；
（2）设直线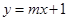
与双曲线C的左支交于A，B两点，另一直线
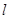经过M（－2，0）及AB的中点，求直线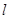在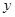
轴上的截距b的取值范围．
已知两曲线参数方程分别为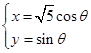
(0≤θ<π)和
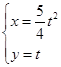( t ∈R)，求它们的交点坐标．
求矩阵A=
的特征值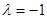
所对应的一个特征向量。
已知点A(1，0)在矩阵M=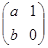
对应变换下变为点B(1，2)，求M－1.
甲有一个箱子，里面放有x个红球，y个白球（x，y≥0，且x+y=4）；乙有一个箱子，里面放有2个红球，1个白球，1个黄球．现在甲从箱子里任取2个球，乙从箱子里任取1个球．若取出的3个球颜色全不相同，则甲获胜．
(1)试问甲如何安排箱子里两种颜色球的个数，才能使自己获胜的概率最大？
(2)在（1）的条件下，求取出的3个球中红球个数的期望．
某地最近出台一项机动车驾照考试规定；每位考试者一年之内最多有4次参加考试的机会，一旦某次考试通过，便可领取驾照，不再参加以后的考试，否则就一直考到第4次为止。如果李明决定参加驾照考试，设他每次参加考试通过的概率依次为0.6，0.7，0.8，0.9，求在一年内李明参加驾照考试次数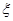
的分布列，并求李明在一年内领到驾照的概率.