已知椭圆中心在原点,焦点在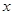 轴上,椭圆短轴的端点和焦点组成的四边形为正方形,且
轴上,椭圆短轴的端点和焦点组成的四边形为正方形,且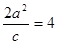 .
.
(1)求椭圆方程;
(2)直线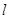 过点
过点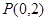 ,且与椭圆相交于
,且与椭圆相交于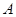 、
、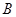 不同的两点,当
不同的两点,当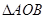 面积取得最大值时,求直线
面积取得最大值时,求直线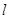 的方程.
的方程.
(本大题满分13分)设函数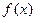 是定义域在
是定义域在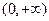 上的单调函数,且对于任意正数
上的单调函数,且对于任意正数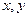 有
有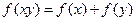 ,已知
,已知 .
.
(1)求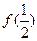 的值;
的值;
(2)一个各项均为正数的数列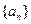 满足:
满足: ,其中
,其中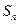 是数列
是数列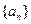 的前n项的和,求数列
的前n项的和,求数列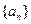 的通项公式;
的通项公式;
(3)在(2)的条件下,是否存在正数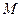 ,使
,使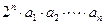


 对一切
对一切 成立?若存在,求出M的取值范围;若不存在,说明理由.
成立?若存在,求出M的取值范围;若不存在,说明理由.
(满分13分)已知椭圆中心在原点,焦点在x轴上,离心率 ,点
,点 分别为椭圆的左、右焦点,过右焦点
分别为椭圆的左、右焦点,过右焦点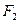 且垂直于长轴的弦长为
且垂直于长轴的弦长为
⑴ 求椭圆的标准方程;
⑵ 过椭圆的左焦点 作直线
作直线 ,交椭圆于
,交椭圆于 两点,若
两点,若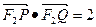 ,求直线
,求直线 的倾斜角。
的倾斜角。
(本小题满分13分)设直线x=1是函数f(x)的图像的一条对称轴,对于任意 ,f(x+2)="--" f(x),当
,f(x+2)="--" f(x),当 .
.
(1)证明:f(x)在R上是奇函数;
(2)当 时,求f(x)的解析式。
时,求f(x)的解析式。
(本小题满分12分)某种商品的生产成本为50元/件,出厂价为60元/件.厂家为了鼓励销售商多订购,决定当一次性订购超过100件时,每多订购一件,所订购全部商品的出厂价就降低0.01元.根据市场调查,销售商一次订购不会超过600件.
(1)设销售商一次订购x件商品时的出厂价为f(x),请写出f(x)的表达式;
(2)当销售商一次订购多少件商品时,厂家获得的利润最大?最大利润是多少?
(本小题满分12分)已知命题P:指数函数f(x)= 在R上单调递减; 命题q:关于x的方程
在R上单调递减; 命题q:关于x的方程 的两个实根均大于0,若
的两个实根均大于0,若 为真,
为真, 为假,求实数a的取值范围。
为假,求实数a的取值范围。