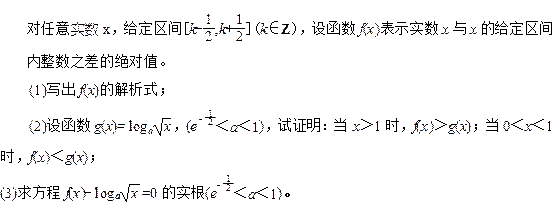（本小题满分14分）已知函数
，函数
的最小值为
，
（1）当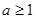
时，求
（2）是否存在实数
同时满足下列条件：①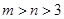
；②当的定义域为
时，值域为
？若存在，求出的值；若不存在，请说明理由。
某班从6名干部中(其中男生4人，女生2人)，选3人参加学校的义务劳动。
(1)设所选3人中女生人数ξ，求ξ的分布列及数学期望；
(2)求男生甲或女生乙被选中的概率；
(3)在男生甲被选中的情况下，求女生乙也被选中的概率。
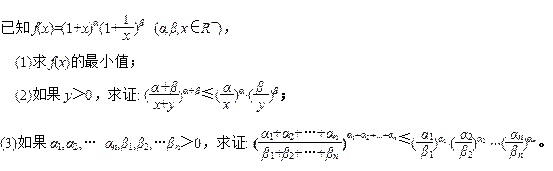
如图，四棱锥P-ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=CD，E是PC的中点。
(1)证明PA平面BDE；
(2)求二面角B-DE-C的平面角的余弦值；
(3)在棱PB上是否存在点F,使PB⊥平面DEF?
证明你的结论。
一袋中有m(m∈N*)个红球，3个黑球和2个白球，现从中任取2个球。
(1)当m=4时，求取出的2个球颜色相同的概率；
(2)当m=3时，设ξ表示取出的2个球中黑球的个数，求ξ的概率分布及数学期望;
(3)如果取出的2个球颜色不相同的概率小于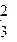
，求m的最小值。
