(本题满分12分)
已知椭圆的中心在原点 ,焦点在坐标轴上,直线
,焦点在坐标轴上,直线 与该椭圆相交于
与该椭圆相交于 和
和 ,且
,且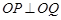 ,
,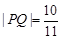 ,求椭圆的方程.
,求椭圆的方程.
已知数列 满足
满足 ,
, ,
, ,其中
,其中 是给定的实数,
是给定的实数, 是正整数,试求
是正整数,试求 的值,使得
的值,使得 的值最小.
的值最小.
将等差数列{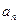 }:
}: 中所有能被3或5整除的数删去后,剩下的数自小到大排成一个数列{
中所有能被3或5整除的数删去后,剩下的数自小到大排成一个数列{ },求
},求 的值.
的值.
六个面分别写上1,2,3,4,5,6的正方体叫做骰子。问
1)共有多少种不同的骰子;
2)骰子相邻两个面上数字之差的绝对值叫做这两个面之间的变差,变差的总和叫做全变差V。在所有的骰子中,求V的最大值和最小值。
一项“过关游戏”规则规定:在第n关要抛掷一颗骰子n次,如果这n次抛掷所出现的点数之和大于 ,则算过关。问:(Ⅰ)某人在这项游戏中最多能过几关?(Ⅱ)他连过前三关的概率是多少?(注:骰子是一个在各面上分别有1,2,3,4,5,6点数的均匀正方体。抛掷骰子落地静止后,向上一面的点数为出现点数。)
,则算过关。问:(Ⅰ)某人在这项游戏中最多能过几关?(Ⅱ)他连过前三关的概率是多少?(注:骰子是一个在各面上分别有1,2,3,4,5,6点数的均匀正方体。抛掷骰子落地静止后,向上一面的点数为出现点数。)
将编号为1,2,…,9的九个小球随机放置在圆周的九个等分点上,每个等分点上各有一个小球.设圆周上所有相邻两球号码之差的绝对值之和为要S.求使S达到最小值的放法的概率.(注:如果某种放法,经旋转或镜面反射后可与另一种放法重合,则认为是相同的放法)