(本小题满分12分)已知椭圆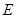 的对称轴为坐标轴,焦点在
的对称轴为坐标轴,焦点在 轴上,离心率
轴上,离心率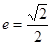 ,
,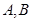 分别为椭圆的上顶点和右顶点,且
分别为椭圆的上顶点和右顶点,且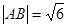 .
.
(Ⅰ)求椭圆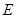 的方程;
的方程;
(Ⅱ)已知直线 与椭圆
与椭圆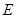 相交于
相交于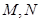 两点,且
两点,且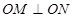 (其中
(其中 为坐标原点),求
为坐标原点),求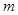 的值.
的值.
已知直线 在矩阵
在矩阵 对应的变换作用下变为直线
对应的变换作用下变为直线 ,求矩阵
,求矩阵 .
.
若数列 中不超过
中不超过 的项数恰为
的项数恰为 (
( ),则称数列
),则称数列 是数列
是数列 的生成数列,称相应的函数
的生成数列,称相应的函数 是数列
是数列 生成
生成 的控制函数.
的控制函数.
(1)已知 ,且
,且 ,写出
,写出 、
、 、
、 ;
;
(2)已知 ,且
,且 ,求
,求 的前
的前 项和
项和 ;
;
(3)已知 ,且
,且 (
( ),若数列
),若数列 中,
中, ,
, ,
, 是公差为
是公差为 (
( )的等差数列,且
)的等差数列,且 ,求
,求 的值及
的值及 的值
的值
已知函数 (
( ),其中
),其中 是自然对数的底数.
是自然对数的底数.
(1)当 时,求
时,求 的极值;
的极值;
(2)若 在
在 上是单调增函数,求
上是单调增函数,求 的取值范围;
的取值范围;
(3)当 时,求整数
时,求整数 的所有值,使方程
的所有值,使方程 在
在 上有解.
上有解.
某隧道设计为双向四车道,车道总宽20米,要求通行车辆限高4.5米,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系 .
.
(1)若最大拱高 为6米,则隧道设计的拱宽
为6米,则隧道设计的拱宽 是多少?
是多少?
(2)为了使施工的土方工程量最小,需隧道口截面面积最小. 现隧道口的最大拱高 不小于6米,则应如何设计拱高
不小于6米,则应如何设计拱高 和拱宽
和拱宽 ,使得隧道口截面面积最小?(隧道口截面面积公式为
,使得隧道口截面面积最小?(隧道口截面面积公式为 )
)
如图,已知椭圆 (
( )的左、右焦点为
)的左、右焦点为 、
、 ,
, 是椭圆上一点,
是椭圆上一点, 在
在 上,且满足
上,且满足 (
( ),
), ,
, 为坐标原点.
为坐标原点.
(1)若椭圆方程为 ,且
,且 ,求点
,求点 的横坐标;
的横坐标;
(2)若 ,求椭圆离心率
,求椭圆离心率 的取值范围
的取值范围