(本小题满分12分)已知等差数列{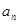 }的公差
}的公差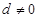 ,它的前n项和为
,它的前n项和为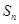 ,若
,若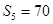 ,且
,且 成等比数列,
成等比数列,
(Ⅰ)求数列{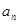 }的通项公式;
}的通项公式;
(Ⅱ)若数列{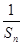 }的前n项和为
}的前n项和为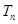 ,求证:
,求证: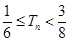 。
。
设不等式|x-2|<a(a∈N*)的解集为A,且 ∈A,
∈A, ∉A.
∉A.
(1)求a的值;
(2)求函数f(x)=|x+a|+|x-2|的最小值.
已知a≥b>0,求证:2a3-b3≥2ab2-a2b.
已知四棱锥P-ABCD的正视图是一个底边长为4,腰长为3的等腰三角形,如图分别是四棱锥P-ABCD的侧视图和俯视图.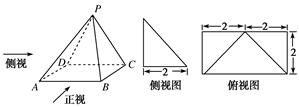
(1)求证:AD⊥PC;
(2)求四棱锥P-ABCD的侧面PAB的面积.
设角A,B,C为△ABC的三个内角.
(1)设f(A)=sin A+2sin 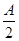 ,当A取A0时,f(A)取极大值f(A0),试求A0和f(A0)的值;
,当A取A0时,f(A)取极大值f(A0),试求A0和f(A0)的值;
(2)当A取A0时,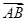 ·
·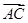 =-1,求BC边长的最小值.
=-1,求BC边长的最小值.
如图,在几何体ABCDE中,AB=AD=2,AB⊥AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,且AE=MC=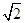 .
.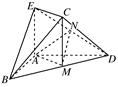
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.