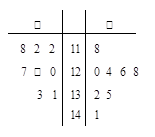在△ABC中, ;(1)求:AB2+AC2的值;(2)当△ABC的面积最大时,求A的大小.
;(1)求:AB2+AC2的值;(2)当△ABC的面积最大时,求A的大小.
已知函数
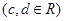 ,其图象为曲线
,其图象为曲线 ,点
,点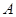 为曲线
为曲线 上的动点,在点
上的动点,在点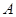 处作曲线
处作曲线 的切线
的切线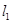 与曲线
与曲线 交于另一点
交于另一点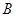 ,在点
,在点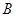 处作曲线
处作曲线 的切线
的切线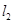 .
.
(Ⅰ)当 时,求函数
时,求函数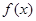 的单调区间;
的单调区间;
(Ⅱ)当点 时,
时,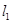 的方程为
的方程为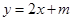 ,求实数
,求实数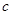 和
和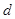 的值;
的值;
(Ⅲ)设切线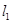 、
、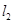 的斜率分别为
的斜率分别为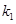 、
、 ,试问:是否存在常数
,试问:是否存在常数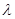 ,使得
,使得 ?若存在,求出
?若存在,求出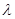 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在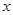 轴上,离心率
轴上,离心率 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线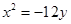 的焦点.
的焦点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 与曲线
与曲线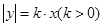 的交点为
的交点为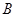 、
、 ,求
,求 面积的最大值.
面积的最大值.
如图,在四棱锥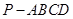 中,
中,  平面
平面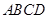 ,
,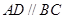 ,
,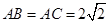 ,
,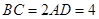 .
.
(Ⅰ)求证: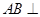 平面
平面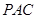 ;
;
(Ⅱ)求棱锥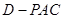 的高.
的高. 
已知数列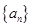 中,点
中,点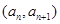
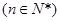 在直线
在直线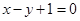 上,且
上,且 .
.
(Ⅰ)求证:数列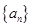 是等差数列,并求
是等差数列,并求 ;
;
(Ⅱ)设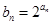 ,数列
,数列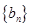 的前
的前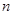 项和为
项和为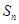 ,
,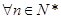 ,
, 成立,求实数
成立,求实数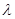 的取值范围.
的取值范围.
某校从参加市联考的甲、乙两班数学成绩110分以上的同学中各随机抽取8人,将这16人的数学成绩编成如下茎叶图.
(Ⅰ)茎叶图中有一个数据污损不清(用△表示),若甲班抽出来的同学平均成绩为122分,试推算这个污损的数据是多少?
(Ⅱ)现要从成绩在130分以上的5位同学中选2位作数学学习方法介绍,请将所有可能的结果列举出来,并求选出的两位同学不在同一个班的概率.