(本小题满分16分)
已知椭圆
 的离心率为
的离心率为 ,一条准线
,一条准线 .
.
(1)求椭圆 的方程;
的方程;
(2)设O为坐标原点, 是
是 上的点,
上的点, 为椭圆
为椭圆 的右焦点,过点F作OM的垂线与以OM为直径的圆
的右焦点,过点F作OM的垂线与以OM为直径的圆 交于
交于 两点.
两点.
①若 ,求圆
,求圆 的方程;
的方程;
②若 是l上的动点,求证:点
是l上的动点,求证:点 在定圆上,并求该定圆的方程.
在定圆上,并求该定圆的方程.
一个多面体的直观图和三视图如图所示,其中M,N分别是AB,AC的中点,G是DF上的一动点.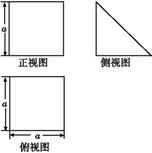
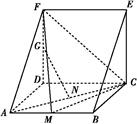
(1)求该多面体的体积与表面积;
(2)求证:GN⊥AC;
(3)当FG=GD时,在棱AD上确定一点P,使得GP∥平面FMC,并给出证明.
如图所示,四棱锥E ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.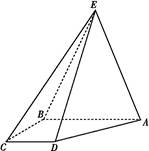
(1)求证:AB⊥ED;
(2)线段EA上是否存在点F,使DF∥平面BCE?若存在,求出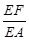 ;若不存在,说明理由.
;若不存在,说明理由.
如图五面体中,四边形ABCD是矩形,DA⊥平面ABEF,AB∥EF,AB=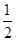 EF=2
EF=2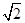 ,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.
,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.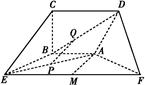
(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面ADF.
如图,四棱锥S ABCD的底面是正方形,每条侧棱的长都是底面边长的
ABCD的底面是正方形,每条侧棱的长都是底面边长的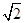 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.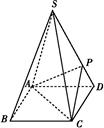
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P AC
AC D的大小;
D的大小;
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE∶EC的值;若不存在,试说明理由.
如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.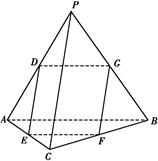
(1)求证:DE∥平面BCP.
(2)求证:四边形DEFG为矩形.
(3)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.