(本小题满分12分)
已知椭圆M的中心为坐标原点,且焦点在x轴上,若M的一个顶点恰好是抛物线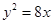 的焦点,M的离心率
的焦点,M的离心率 ,过M的右焦点F作不与坐标轴垂直的直线
,过M的右焦点F作不与坐标轴垂直的直线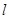 ,交M于A,B两点。
,交M于A,B两点。
(1)求椭圆M的标准方程;
(2)设点N(t,0)是一个动点,且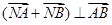 ,求实数t的取值范围。
,求实数t的取值范围。
(本题满分14分) 设等差数列{an}的首项a1为a,公差d=2,前n项和为Sn.
(Ⅰ) 若S1,S2,S4成等比数列,求数列{an}的通项公式;
(Ⅱ) 证明: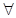 n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
(本题满分14分) 设向量α=(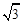 sin 2x,sin x+cos x),β=(1,sin x-cos x),其中x∈R,函数f (x)=α
sin 2x,sin x+cos x),β=(1,sin x-cos x),其中x∈R,函数f (x)=α β.(Ⅰ) 求f (x) 的最小正周期;(Ⅱ) 若f (θ)=
β.(Ⅰ) 求f (x) 的最小正周期;(Ⅱ) 若f (θ)= ,其中0<θ<
,其中0<θ< ,求cos(θ+
,求cos(θ+ )的值.
)的值.
已知圆心角为120° 的扇形AOB半径为 ,C为
,C为 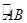 中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2=2,则OD+OE的最大值是.
中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2=2,则OD+OE的最大值是.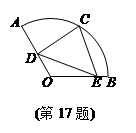
如图,椭圆C: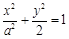 的焦点在x轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线
的焦点在x轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线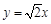 上一点P.
上一点P.
(1)求椭圆C及抛物线C1、C2的方程;
(2)若动直线l与直线OP垂直,且与椭圆C交于不同两点M、N,已知点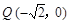 ,求
,求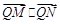 的最小值.
的最小值.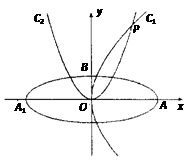
若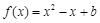 ,且
,且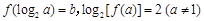 .
.
(1)求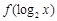 的最小值及对应的x值;
的最小值及对应的x值;
(2)若不等式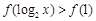 的解集记为A,不等式
的解集记为A,不等式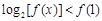 的解集记为B,求
的解集记为B,求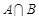 .
.