(本小题满分8分)如图,A(2,1)是矩形OCBD的对角线OB上的一点,点E在BC上,双曲线y= 经过点A,交BC于点E,交BD于点F,若CE=
经过点A,交BC于点E,交BD于点F,若CE= .
.
(1)求双曲线的解析式;
(2)求点F的坐标;
(3)连接EF、DC,求证:EF∥DC.
(本小题满分6分)小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.
根据图中的数据(单位:m),解答下列问题:
(1)用含x、y的代数式表示地面总面积;
(2)小王发现客厅面积比卫生间面积大21m2,且地面总面积是卫生间面积的15倍.若铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
(本小题满分6分)如上图,在△ABC和△EDC中,AC=CE=CB=CD,∠ACB=∠ECD=90°,AB与CE交于F,ED与AB、BC分别交于M、H.
(1)求证:CF=CH;
(2)如下图,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM是什么四边形?并证明你的结论.
(本小题满分6分)“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
(满分10分)如图,已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C.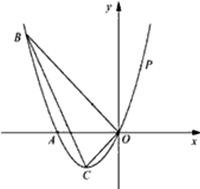
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)P是抛物线上的第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.