某校高三年级进行了一次数学测验,随机从甲乙两班各抽取6名同学,所得分数的茎叶图如右图所示:
(I)根据茎叶图判断哪个班的平均分数较高,并说明理由;
(II)现从甲班这6名同学中随机抽取两名同学,求他们的分数之和大于165分的概率.
已知集合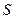 ={
={ |
| 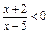 },
}, ={
={ |
| 

 },
},
(Ⅰ)求集合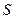 ;
;
(Ⅱ)若 ,求实数a的取值范围.
,求实数a的取值范围.
如图,已知正方体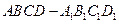 的棱长为2,E、F分别是
的棱长为2,E、F分别是 、
、 的中点,过
的中点,过 、E、F作平面
、E、F作平面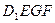 交
交 于G..
于G..
(Ⅰ)求证: ∥
∥ ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)求正方体被平面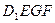 所截得的几何体
所截得的几何体 的体积.
的体积.
已知圆C: ,圆C关于直线
,圆C关于直线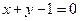 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为
(Ⅰ)求圆C的方程;
(Ⅱ)已知不过原点的直线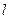 与圆C相切,且在x轴、y轴上的截距相等,求直线
与圆C相切,且在x轴、y轴上的截距相等,求直线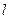 的方程。
的方程。
在一次考试中共有8道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.评分标准规定:“每题只选一个选项,选对得5分,不选或选错得0分”.某考生已确定有4道题答案是正确的,其余题中:有两道只能分别判断2个选项是错误的,有一道仅能判断1个选项是错误的,还有一道因不理解题意只好乱猜,求:
(1)该考生得40分的概率;
(2)该考生得多少分的可能性最大?
(3)该考生所得分数的数学期望.