求过点A(-1,2),且到原点的距离等于 的直线l的方程.
的直线l的方程.
为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物.某人一次种植了n株沙柳.各株沙柳的成活与否是相互独立的,成活率为p,设 为成活沙柳的株数,数学期望E(
为成活沙柳的株数,数学期望E( )为3,标准差
)为3,标准差 为
为 .
.
(1)求n和p的值,并写出 的概率分布;
的概率分布;
(2)若有3株或3株以上的沙柳未成活,则需要补种.求需要补种沙柳的概率.
灯泡厂生产的白炽灯寿命X(单位:h),已知X~N(1 000,302),要使灯泡的平均寿命为1 000 h的概率为99.7%,问灯泡的平均寿命应控制在多少小时以上?
某人乘车从A地到B地,所需时间(分钟)服从正态分布N(30,100),求此人在40分钟至50分钟到达目的地的概率.
某地位于甲、乙两条河流的交汇处,根据统计资料预测,今年汛期甲河流发生洪水的概率为0.25,乙河流发生洪水的概率为0.18(假设两河流发生洪水与否互不影响).现有一台大型设备正在该地工作,为了保护设备,施工部门提出以下三种方案:
方案1:运走设备,此时需花费4 000元;
方案2:建一保护围墙,需花费1 000元,但围墙只能抵御一个河流发生的洪水,当两河流同时发生洪水时,设备仍将受损,损失约56 000元;
方案3:不采取措施,此时,当两河流都发生洪水时损失达60 000元,只有一条河流发生洪水时,损失为10 000元.
(1)试求方案3中损失费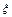 (随机变量)的概率分布;
(随机变量)的概率分布;
(2)试比较哪一种方案好.