已知⊙O1经过 ,
, ,
, ,
, 四点,一次函数
四点,一次函数 的图象是直线
的图象是直线 ,直线
,直线 与
与 轴交于点
轴交于点 .
.
(1)在如图的平面直角坐标系中画出直线l,则直线 与⊙O1的交点坐标为 _______________ ;
与⊙O1的交点坐标为 _______________ ;
(2)若⊙O1上存在整点 (横坐标与纵坐标均为整数的点称
(横坐标与纵坐标均为整数的点称
为整点),使得 为等腰三角形,所有满足条件的点
为等腰三角形,所有满足条件的点 的坐标为 _____________ ;
的坐标为 _____________ ;
(3)将 沿X轴向右平移 个单位时,
沿X轴向右平移 个单位时, 与y轴相切
与y轴相切
如图,在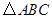 中,
中,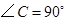 ,在
,在 边上取一点
边上取一点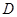 ,使
,使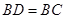 ,过
,过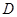 作
作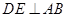 交AC于E,AC=8,BC=6.求DE的长.
交AC于E,AC=8,BC=6.求DE的长.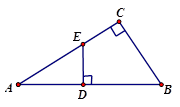
以直线 为对称轴的抛物线过点A(3,0)和点B(0,3),求此抛物线的解析式.
为对称轴的抛物线过点A(3,0)和点B(0,3),求此抛物线的解析式.
如图:已知,梯形ABCD中,∠B=90°,AD∥BC,AB⊥BC,AB=AD=3,BC= 7.
7.
求cos∠C.
已知抛物线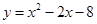 .
.(1)用配方法把
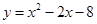 化为
化为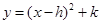 形式;
形式;(2)并指出:抛物线的顶点坐标是,抛物线的对称轴方程是,
抛物线与x轴交点坐标是,当x时,y随x的增大而增大.
解
( 本题12分) 已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E。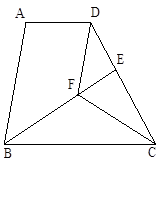
求证:(1)△BFC≌△DFC;
(2)AD=DE