设椭圆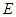 :
: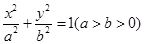 的左、右焦点分别为
的左、右焦点分别为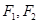 ,已知椭圆
,已知椭圆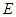 上的任意一点
上的任意一点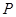 ,满足
,满足 ,过
,过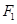 作垂直于椭圆长轴的弦长为3.
作垂直于椭圆长轴的弦长为3.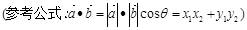
(1)求椭圆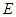 的方程;
的方程;
(2)若过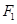 的直线交椭圆于
的直线交椭圆于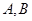 两点,求
两点,求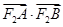 的取值范围.
的取值范围.
已知函数 ,(
,( >0,
>0, ,以点
,以点 为切点作函数
为切点作函数 图象的切线
图象的切线 ,记函数
,记函数 图象与三条直线
图象与三条直线 所围成的区域面积为
所围成的区域面积为 .
.
(1)求 ;
;
(2)求证: <
< ;
;
(3)设 为数列
为数列 的前
的前 项和,求证:
项和,求证: <
< .来
.来
某市质监部门对市场上奶粉进行质量抽检,现将9个进口品牌奶粉的样品编号为1,2,3,4, ,9;6个国产品牌奶粉的样品编号为10,11,12,15,按进口品牌及国产品牌分层进行分层抽样,从其中抽取5个样品进行首轮检验,用 表示编号为
表示编号为
 的样品首轮同时被抽到的概率.
的样品首轮同时被抽到的概率.
(1)求 的值;
的值;
(2)求所有的
 的和.
的和.
已知椭圆 的右焦点为
的右焦点为 ,设左顶点为A,上顶点为B且
,设左顶点为A,上顶点为B且 ,如图.
,如图.
(1)求椭圆 的方程;
的方程;
(2)若 ,过
,过 的直线
的直线 交椭圆于
交椭圆于 两点,试确定
两点,试确定 的取值范围.
的取值范围.
已知函数 在
在 处取得极小值.
处取得极小值.
(1)若函数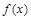 的极小值是
的极小值是 ,求
,求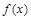 ;
;
(2)若函数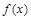 的极小值不小于
的极小值不小于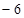 ,问:是否存在实数
,问:是否存在实数 ,使得函数
,使得函数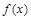 在
在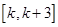 上单调递减?若存在,求出
上单调递减?若存在,求出 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB= AB.直角梯形ACEF中,
AB.直角梯形ACEF中,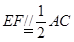 ,
, 是锐角,且平面ACEF⊥平面ABCD.
是锐角,且平面ACEF⊥平面ABCD.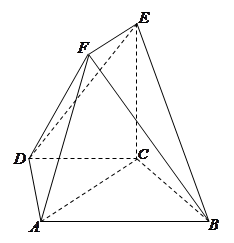
(1)求证: ;
;
(2)若直线DE与平面ACEF所成的角的正切值是 ,试求
,试求 的余弦值.
的余弦值.