在ΔABC中，角A、B、C所对的边分别为a，b，c，且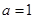
，
，
。
（1）求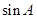
的值；
（2）求ΔABC的面积。
如图，三棱锥P-ABC中，PA⊥底面ABC，AB⊥BC，DE垂直平分线段PC，且分别交AC、PC于D、E两点,又PB
=BC，PA=AB。
（1）求证：PC⊥平面BDE；
（2）若点Q是线段PA上任一点，判断BD、DQ的位置关系，并证明你的结论；
（3）若AB=2,求三棱锥B-CED的体积
为了迎接省运会，为了降低能源损耗，鹰潭市体育馆的外
墙需要建造隔热层．体育馆要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度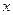
（单位：cm）满足关系：
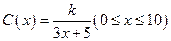，若不建隔热层，每年能源消耗费用为8万元．设
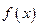为隔热层建造费用与20年的能源消
耗费用之和．
（1）求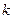
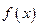的值及的表达式；
（2）隔热层修建多厚时，总费用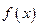达到最小，并求最小值
在△ABC中，内角A，B，C所对边长分别为
，
，
，
.
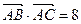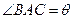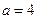（1）求
的最大值及
的取值范围；
（2）求函数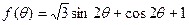
的最大值和最小值.
已知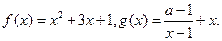
（I）a=2时，求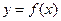
和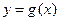
的公共点个数；
（II）a为何值时，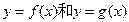
的公共点个数恰为两个。
已知椭圆
的右焦点为F2（1，0），点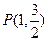
在椭圆上。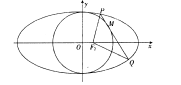
（I）求椭圆方程；
（II）点
在圆
上，M在第一象限，过M作圆的切线交椭圆于P、Q两点，问|F2P|+|F2Q|+|PQ|是否为定值？如果是，求出定值，如不是，说明理由。