在直角坐标系xOy中,直线l的方程为x-y+4=0,曲线C的参数方程为 (α为参数).
(α为参数).
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,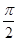 ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
已知直线 ,一个圆的圆心
,一个圆的圆心 在
在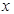 轴正半轴上,且该圆与直线
轴正半轴上,且该圆与直线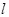 和
和 轴均相切.
轴均相切.
(1)求该圆的方程;
(2)直线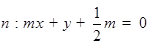 与圆
与圆 交于
交于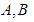 两点,且
两点,且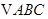 是等边三角形,求
是等边三角形,求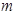 的值.
的值.
2010年上海世博会某国要建一座八边形(不一定为正八边形)的展馆区(如图),它的主体造型的平面图是由二个相同的矩形 和
和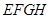 构成的面积为
构成的面积为 m2的十字型地域,计划在正方形
m2的十字型地域,计划在正方形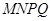 上建一座“观景花坛”,造价为
上建一座“观景花坛”,造价为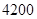 元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为
元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为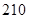 元/m2,再在四个空角(如
元/m2,再在四个空角(如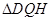 等)上铺草坪,造价为
等)上铺草坪,造价为 元/m2.设总造价为
元/m2.设总造价为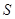 元,
元,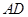 长为
长为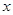 m.
m.
(1)试建立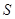 与
与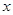 的函数关系
的函数关系
(2)当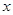 为何值时,
为何值时, 最小?并求这个最小值
最小?并求这个最小值
如下图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.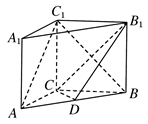
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求三棱锥 的体积.
的体积.
在锐角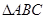 中,已知内角
中,已知内角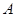 ,
, ,
, 所对的边分别为
所对的边分别为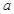 ,
, ,
, ,向量
,向量
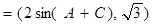 ,
,
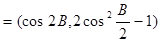 ,且向量
,且向量 共线.
共线.
(1)求角 的大小;
的大小;
(2)如果 ,求
,求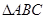 的周长的最大值.
的周长的最大值.
(本小题满分10分)已知数列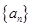 的各项均为正整数,对于任意n∈N*,都有
的各项均为正整数,对于任意n∈N*,都有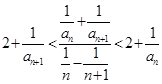 成立,且
成立,且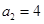 .
.
(1)求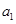 ,
,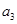 的值;
的值;
(2)猜想数列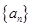 的通项公式,并给出证明.
的通项公式,并给出证明.