已知曲线 y = x3 + x-2 在点 P0 处的切线  与直线4x-y-1=0平行,且点 P0 在第三象限,
与直线4x-y-1=0平行,且点 P0 在第三象限,
(1)求P0的坐标;
(2)若直线 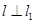 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
如图,在三棱锥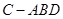 中,
中,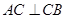 ,
,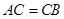 ,
,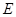 为
为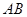 的中点,
的中点,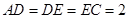 ,
,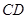 =
=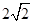 .
.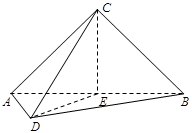
(1)求证:平面 ⊥平面
⊥平面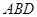 ;
;
(2)求直线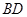 与平面
与平面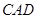 所成角的正弦值.
所成角的正弦值.
甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动,在本次海选中有合格和不合格两个等级.若海选合格记1分,海选不合格记0分.假设甲、乙、丙海选合格的概率分别为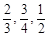 ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的.
(1)求在这次海选中,这三名音乐爱好者至少有一名海选合格的概率;
(2)记在这次海选中,甲、乙、丙三名音乐爱好者所得分之和为随机变量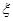 ,求随机变量
,求随机变量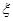 的分布列和数学期望
的分布列和数学期望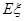 .
.
已知函数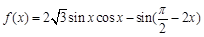 ,
,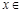 R.
R.
(1)求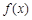 的最小值,并求出相应的
的最小值,并求出相应的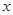 值的集合;
值的集合;
(2)求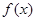 的单调递减区间.
的单调递减区间.
已知函数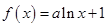 ,
,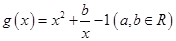 .
.
(1)若曲线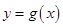 在点
在点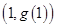 处的切线平行于
处的切线平行于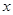 轴,求
轴,求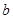 的值;
的值;
(2)当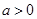 时,若对
时,若对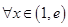 ,
,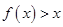 恒成立,求实数
恒成立,求实数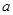 的取值范围;
的取值范围;
(3)设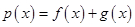 ,在(1)的条件下,证明当
,在(1)的条件下,证明当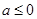 时,对任意两个不相等的正数
时,对任意两个不相等的正数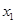 、
、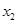 ,有
,有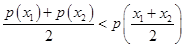 .
.
已知正项数列 满足:
满足: ,数列
,数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.