如图,一个梯子AB长2.5 米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,求梯子顶端A下落了多少米?
某中学抽取了40名学生参加"平均每周课外阅读时间"的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
频数分布表
|
组别 |
时间/小时 |
频数/人数 |
|
A组 |
0≤ t<1 |
2 |
|
B组 |
1≤ t<2 |
m |
|
C组 |
2≤ t<3 |
10 |
|
D组 |
3≤ t<4 |
12 |
|
E组 |
4≤ t<5 |
7 |
|
F组 |
t≥5 |
4 |
请根据图表中的信息解答下列问题:
(1)求频数分布表中 m的值;
(2)求 B组, C组在扇形统计图中分别对应扇形的圆心角度数,并补全扇形统计图;
(3)已知 F组的学生中,只有1名男生,其余都是女生,用列举法求以下事件的概率:从 F组中随机选取2名学生,恰好都是女生.

已知 P= ﹣ ( a≠± b)
(1)化简 P;
(2)若点( a, b)在一次函数 y= x﹣ 的图象上,求 P的值.
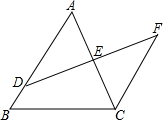
如图, D是 AB上一点, DF交 AC于点 E, DE= FE, FC∥ AB,求证:△ ADE≌△ CFE.
已知Rt△ OAB,∠ OAB=90°,∠ ABO=30°,斜边 OB=4,将Rt△ OAB绕点 O顺时针旋转60°,如图1,连接 BC.
(1)填空:∠ OBC= °;
(2)如图1,连接 AC,作 OP⊥ AC,垂足为 P,求 OP的长度;
(3)如图2,点 M, N同时从点 O出发,在△ OCB边上运动, M沿 O→ C→ B路径匀速运动, N沿 O→ B→ C路径匀速运动,当两点相遇时运动停止,已知点 M的运动速度为1.5单位/秒,点 N的运动速度为1单位/秒,设运动时间为 x秒,△ OMN的面积为 y,求当 x为何值时 y取得最大值?最大值为多少?

如图,四边形 ABCD中, AB= AD= CD,以 AB为直径的⊙ O经过点 C,连接 AC、 OD交于点 E.
(1)证明: OD∥ BC;
(2)若tan∠ ABC=2,证明: DA与⊙ O相切;
(3)在(2)条件下,连接 BD交⊙ O于点 F,连接 EF,若 BC=1,求 EF的长.
