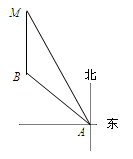
如图,我边防哨所A测得一走私船在A的西北方向B处由南向北正以每小时10海里的速度逃跑,我缉私艇迅速朝A的西偏北600的方向出水拦截,2小时后终于在B地正北方向M处拦截住,试求缉私船的速度.(参考数据: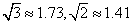 )
)
如图,延长 的边 到 ,使 ,延长 到点 ,使 ,分别连接点 、 和 、 .求证: .

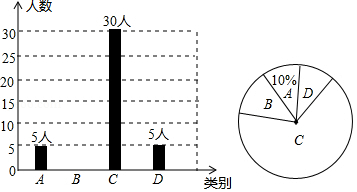
随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别: 步)(说明:“ ”表示大于等于0,小于等于5000,下同), 步), 步), 步以上),统计结果如图所示:
请依据统计结果回答下列问题:
(1)本次调查中,一共调查了 位好友.
(2)已知 类好友人数是 类好友人数的5倍.
①请补全条形图;
②扇形图中,“ ”对应扇形的圆心角为 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?

央视“经典咏流传”开播以来受到社会广泛关注我市某校就“中华文化我传承 地方戏曲进校园”的喜爱情况进行了随机调查.对收集的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
图中 表示“很喜欢”, 表示“喜欢”、 表示“一般”, 表示“不喜欢”.
(1)被调查的总人数是 人,扇形统计图中 部分所对应的扇形圆心角的度数为 ;
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中 类有 人;
(4)在抽取的 类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
为了解某校九年级男生1000米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为 、 、 、 四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:

(1) , , ;
(2)扇形统计图中表示 等次的扇形所对的圆心角的度数为 度;
(3)学校决定从 等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生1000米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
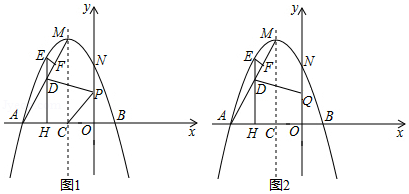
在平面直角坐标系中,抛物线 与 轴交于点 、 ,交 轴于点 ,点 为抛物线的顶点,对称轴与 轴交于点 .
(1)求抛物线的解析式;
(2)如图1,连接 ,点 是线段 上方抛物线上一动点, 于点 ,过点 作 轴于点 ,交 于点 .点 是 轴上一动点,当 取最大值时:
①求 的最小值;
②如图2, 点为 轴上一动点,请直接写出 的最小值.