把下列方程化为直角坐标方程(并说明对应的曲线):
① ②
②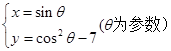
甲、乙两人参加某种选拔测试.在备选的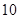 道题中,甲答对其中每道题的概率都是
道题中,甲答对其中每道题的概率都是 ,乙能答对其中的
,乙能答对其中的 道题.规定每次考试都从备选的
道题.规定每次考试都从备选的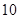 道题中随机抽出
道题中随机抽出 道题进行测试,答对一题加
道题进行测试,答对一题加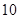 分,答错一题(不答视为答错)减
分,答错一题(不答视为答错)减 分,至少得
分,至少得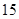 分才能入选.
分才能入选.
(1)求甲得分的数学期望;
(2)求甲、乙两人同时入选的概率.
已知公差不为0的等差数列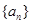 的前
的前 项和为
项和为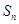 ,
, ,且
,且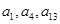 成等比数列.
成等比数列.
(1)求数列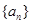 的通项公式;
的通项公式;
(2)试推导数列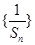 的前
的前 项和
项和 的表达式。
的表达式。
已知向量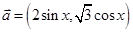 ,
, ,函数
,函数
(1)求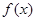 的单调递增区间;
的单调递增区间;
(2)若不等式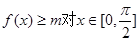 都成立,求实数m的最大值.
都成立,求实数m的最大值.
设函数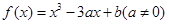 .
.
(1)若曲线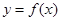 在点
在点 处与直线
处与直线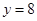 相切,求
相切,求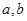 的值;
的值;
(2)求函数 的单调区间与极值点.
的单调区间与极值点.
(3)设函数 的导函数是
的导函数是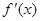 ,当
,当 时求证:对任意
时求证:对任意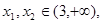
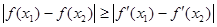 成立
成立
已知在平面直角坐标系 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为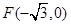 ,右顶点为
,右顶点为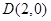 ,设点
,设点 .
.
(1)求该椭圆的标准方程;
(2)若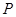 是椭圆上的动点,求线段
是椭圆上的动点,求线段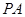 中点
中点 的轨迹方程;
的轨迹方程;