如图1，已知点B（1，3）、C（1，0），直线y=x+k经过点B，且与x轴交于点A，将△ABC沿直线AB折叠得到△ABD.
（1）填空：A点坐标为（____，____），D点坐标为（____，____）；
（2）若抛物线y= 
x2+bx+c经过C、D两点，求抛物线的解析式；
（3）将（2）中的抛物线沿y轴向上平移，设平移后所得抛物线与y轴交点为E，点M是平移后的抛物线与直线AB的公共点，在抛物线平移过程中是否存在某一位置使得直线EM∥x轴.若存在，此时抛物线向上平移了几个单位？若不存在，请说明理由.
如图：在正方形网格中有一个△ABC，请按下列要求进行（只能借助于网格）：
（1）、请作出△ABC中BC边上的高AE；
（2）、作出将△ABC向右平移6格，再向上平移3格后的△DEF；
（3）、作一个锐角△MNP（要求各顶点在格点上），使其面积等于△ABC的面积。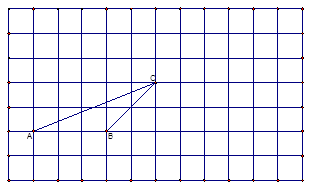
如图，在△ABC中，点D为BC边上的点，BE平分∠ABC交AD于点E．若∠ABE=15°，∠BAD=40°，求∠ADC的度数。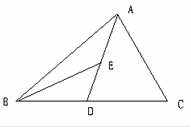
如图，M是AB的中点，∠C=∠D，∠1=∠2，请说明 AC=BD的理由（填空）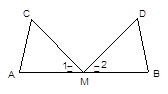
解：
M是AB的中点，
∴ AM = ( )
在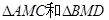
中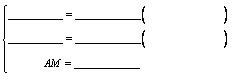
∴△≌△（）
∴AC=BD（）
解下列方程组：
（1）
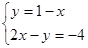；（2）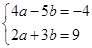
计算：4.7－（－8.9）－7.5+（－6）；