某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是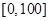 ,样本数据分组为
,样本数据分组为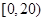 ,
,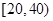 ,
,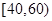 ,
,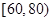 ,
,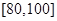 .
.
(Ⅰ)求直方图中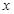 的值;
的值;
(Ⅱ)如果上学所需时间不少于1小时的学生可申请在学校住宿,请估计学校600名新生中有多少名学生可以申请住宿;
(Ⅲ)从学校的新生中任选4名学生,这4名学生中上学所需时间少于20分钟的人数记为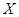 ,求
,求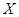 的分布列和数学期望.(以直方图中新生上学所需时间少于20分钟的频率作为每名学生上学所需时间少于20分钟的概率)
的分布列和数学期望.(以直方图中新生上学所需时间少于20分钟的频率作为每名学生上学所需时间少于20分钟的概率)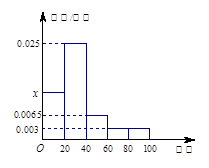
在四棱锥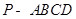 中,
中,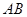 //
//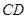 ,
,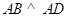 ,
,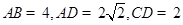 ,
,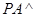 平面
平面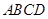 ,
,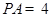 .
.
(Ⅰ)设平面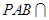 平面
平面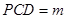 ,求证:
,求证: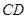 //
// ;
;
(Ⅱ)求证: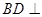 平面
平面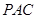 ;
;
(Ⅲ)设点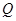 为线段
为线段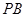 上一点,且直线
上一点,且直线 与平面
与平面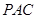 所成角的正弦值为
所成角的正弦值为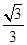 ,求
,求 的值.
的值.
在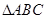 中,角
中,角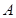 ,
,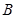 ,
, 的对边分别为
的对边分别为 ,且
,且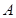 ,
,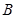 ,
, 成等差数列.
成等差数列.
(Ⅰ)若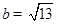 ,
,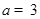 ,求
,求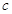 的值;
的值;
(Ⅱ)设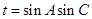 ,求
,求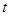 的最大值.
的最大值.
已知各项均为非负整数的数列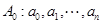
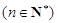 ,满足
,满足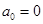 ,
, .若存在最小的正整数
.若存在最小的正整数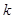 ,使得
,使得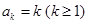 ,则可定义变换
,则可定义变换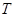 ,变换
,变换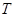 将数列
将数列 变为数列
变为数列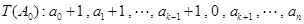 .设
.设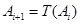 ,
,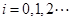 .
.
(Ⅰ)若数列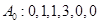 ,试写出数列
,试写出数列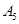 ;若数列
;若数列 ,试写出数列
,试写出数列 ;
;
(Ⅱ)证明存在唯一的数列 ,经过有限次
,经过有限次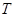 变换,可将数列
变换,可将数列 变为数列
变为数列 ;
;
(Ⅲ)若数列 ,经过有限次
,经过有限次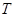 变换,可变为数列
变换,可变为数列 .设
.设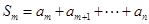 ,
,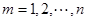 ,求证
,求证 ,其中
,其中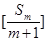 表示不超过
表示不超过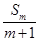 的最大整数.
的最大整数.
已知椭圆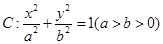 的两个焦点分别为
的两个焦点分别为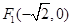 ,
,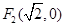 .点
.点 与椭圆短轴的两个端点的连线相互垂直.
与椭圆短轴的两个端点的连线相互垂直.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知点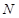 的坐标为
的坐标为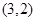 ,点
,点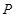 的坐标为
的坐标为 .过点
.过点 任作直线
任作直线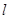 与椭圆
与椭圆 相交于
相交于 ,
,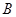 两点,设直线
两点,设直线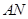 ,
,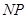 ,
,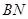 的斜率分别为
的斜率分别为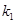 ,
,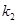 ,
,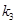 ,若
,若 ,试求
,试求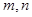 满足的关系式.
满足的关系式.