已知数列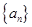 是首项
是首项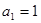 的等比数列,其前
的等比数列,其前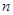 项和
项和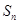 中,
中,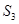 、
、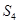 、
、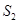 成等差数列.
成等差数列.
(1)求数列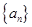 的通项公式;
的通项公式;
(2)设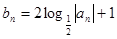 ,求数列{
,求数列{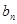 }的前
}的前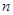 项和为
项和为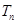 ;
;
(3)求满足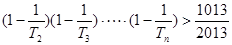 的最大正整数
的最大正整数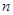 的值.
的值.
(本小题满分8分)
已知函数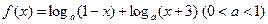
(1)求函数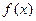 的定义域;
的定义域;
(2)求函数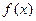 的零点;
的零点;
(3)若函数f(x)的最小值为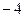 ,求
,求 的值.
的值.
(本小题满分8分)
计算求值
(1) 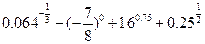
(2) 
(本小题满分8分)
设全集U="{1," 2, 3, 4, 5}, 集合A="{1," a2-1, 4},  ="{2," a+3}
="{2," a+3}
(I)求a值;
(II)满足AÍBU这样的集合B共有几个?试将这样的B集合都写出来
(文科做)
设集合 ,
,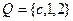 ,且满足
,且满足 , 若
, 若 .
.
(Ⅰ) 求b = c的概率;
(Ⅱ)求方程 有实根的概率
有实根的概率
(理科做)设函数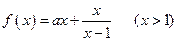
(1)若a>0,求函数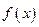 的最小值;
的最小值;
(2)若a是从1,2,3三个数中任取一个数,b是从2,3,4,5四个数中任取一个数,
求f (x)>b恒成立的概率