某算法的程序框图如图所示，其中输入的变量 在1，2，3，…，24这24个整数中等可能随机产生．
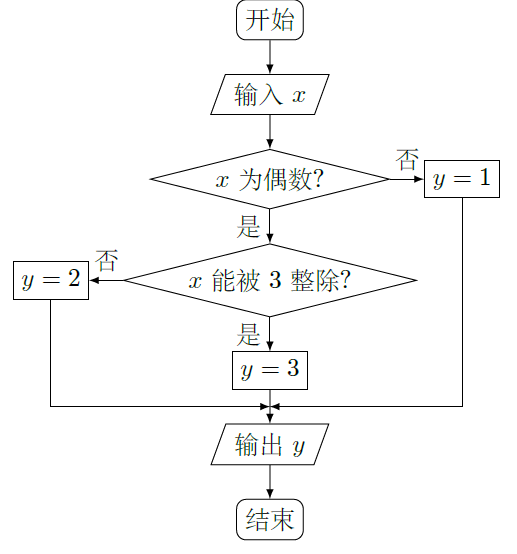
（Ⅰ）分别求出按程序框图正确编程运行时输出
的值为
的概率
（
=1，2，3）；
（Ⅱ）甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行
次后，统计记录了输出
的值为
（
=1，2，3）的频数．以下是甲、乙所作频数统计表的部分数据．
甲的频数统计表（部分）
| 运行 次数 |
输出
的值 为1的频数 |
输出
的值 为2的频数 |
输出
的值 为3的频数 |
| 30 |
14 |
6 |
10 |
| … |
… |
… |
… |
| 2100 |
1027 |
376 |
697 |
乙的频数统计表（部分）
| 运行 次数 |
输出
的值 为1的频数 |
输出
的值 为2的频数 |
输出
的值 为3的频数 |
| 30 |
12 |
11 |
7 |
| … |
… |
… |
… |
| 2100 |
1051 |
696 |
353 |
当n=2100时，根据表中的数据，分别写出甲、乙所编程序各自输出 的值为 （ =1，2，3）的频率（用分数表示），并判断两位同学中哪一位所编写程序符合算法要求的可能性较大．
设是等差数列，是各项都为正整数的等比数列，且，
，
，
．
（Ⅰ）求，的通项公式；
（Ⅱ）若数列
满足
（），且
，试求的通项公式及其前
项和
．
如图，在正四棱台
中，
，
，
，
、
分别是
、
的中点. 
（Ⅰ）求证：平面
∥平面
；
（Ⅱ）求二面角
的余弦值的大小.
注：底面为正方形，从顶点向底面作垂线，垂足是底面中心，这样的四棱锥叫做正四棱锥.用一个平行于正四棱锥底面的平面去截该棱锥，底面与截面之间的部分叫做正四棱台.
为了分流地铁高峰的压力，某市发改委通过听众会，决定实施低峰优惠票价制度.不超过
公里的地铁票价如下表：
乘坐里程 （单位： ） |
 |
 |
 |
| 票价（单位：元） |
 |
 |
 |
现有甲、乙两位乘客，他们乘坐的里程都不超过公里.已知甲、乙乘车不超过
公里的概率分别为
，
，甲、乙乘车超过公里且不超过
公里的概率分别为
，.
（Ⅰ）求甲、乙两人所付乘车费用不相同的概率；
（Ⅱ）设甲、乙两人所付乘车费用之和为随机变量
，求的分布列与数学期望．
已知向量
,
,实数
为大于零的常数，函数
,
，且函数
的最大值为
.
（Ⅰ）求的值；
（Ⅱ）在
中，
分别为内角
所对的边，若
，
,且
,求
的最小值.
（本小题满分10分）
已知集合A是集合Pn＝{1，2，3， ，n} (n≥3，n∈N*)的子集，且A中恰有3个元素，同时这3个元素的和是3的倍数．记符合上述条件的集合A的个数为f(n)．
（1）求f(3)，f(4)；
（2）求f(n)（用含n的式子表示）．