如图,在各棱长均为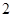 的三棱柱
的三棱柱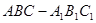 中,侧面
中,侧面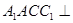 底面
底面 ,
, .
.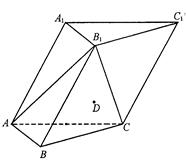
(1)求侧棱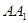 与平面
与平面 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)已知点 满足
满足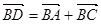 ,在直线
,在直线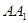 上是否存在点
上是否存在点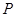 ,使
,使 ?若存在,请确定点
?若存在,请确定点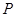 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(本题满分10分)已知圆 过点
过点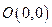 ,
,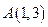 ,
,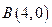 .
.
(1)求圆 的方程;
的方程;
(2)设直线 :
: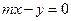 ,
, :
: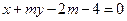 的交点为
的交点为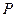 ,求证:点
,求证:点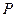 必
必
圆 上.
上.
(本题满分8分)已知两直线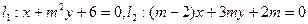 ,
,
当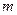 为何值时,
为何值时,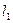 与
与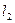 重合?
重合?
(本小题满分14分)
已知两定点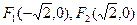 ,若点P满足
,若点P满足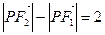 。
。
(1)求点P的轨迹及其方程。
(2)直线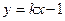 与点P的轨迹交于A、B两点,若
与点P的轨迹交于A、B两点,若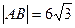 ,且曲线E上存在点C,使
,且曲线E上存在点C,使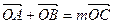 ,求实数
,求实数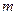
(本小题满分12分)
|
如图,在四棱锥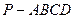 中,
中,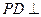 面ABCD,ABCD为矩形,AD=
面ABCD,ABCD为矩形,AD=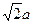 ,PD=DC=
,PD=DC=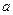 ,M、N分别为AD、PB的中点。
,M、N分别为AD、PB的中点。
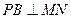 ;
;
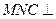 平面
平面 ;
;
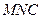 的距离。
的距离。
(本小题满分12分)
设抛物线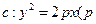 >0)上有两动点A、B(AB不垂直
>0)上有两动点A、B(AB不垂直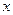 轴),F为焦点,且
轴),F为焦点,且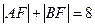 ,又线段AB的垂直平分线经过定点Q(6,0),求抛物线方程。
,又线段AB的垂直平分线经过定点Q(6,0),求抛物线方程。