如图1,四棱锥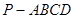 中,
中,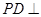 底面
底面 ,面
,面 是直角梯形,
是直角梯形,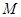 为侧棱
为侧棱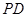 上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
(Ⅰ)证明: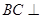 平面
平面 ;
;
(Ⅱ)证明: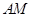 ∥平面
∥平面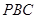 ;
;
(Ⅲ)线段 上是否存在点
上是否存在点 ,使
,使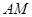 与
与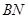 所成角的余弦值为
所成角的余弦值为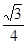 ?若存在,找到所有符合要求的点
?若存在,找到所有符合要求的点 ,并求
,并求 的长;若不存在,说明理由.
的长;若不存在,说明理由.
(本小题满分14分)已知函数 满足
满足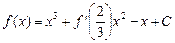 (其中
(其中 为
为 在点
在点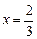 处的导数,
处的导数, 为常数).(1)求函数
为常数).(1)求函数 的单调区间;(2)若方程
的单调区间;(2)若方程 有且只有两个不等的实数根,求常数
有且只有两个不等的实数根,求常数 ;(3)在(2)的条件下,若
;(3)在(2)的条件下,若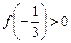 ,求函数
,求函数 的图象与
的图象与 轴围成的封闭图形的面积.
轴围成的封闭图形的面积.
(本小题满分12分)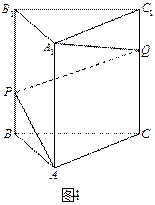 如图4,正三棱柱
如图4,正三棱柱 中,
中, ,
,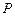 、
、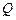 分别是侧棱
分别是侧棱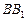 、
、 上的点,且使得折线
上的点,且使得折线 的长
的长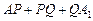 最短.
最短.
(1)证明:平面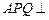 平面
平面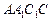 ;(2)求直线
;(2)求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.
(本小题满分12分)设有同频率的两个正弦电流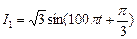 ,
,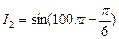 ,把它们合成后,得到电流
,把它们合成后,得到电流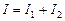 .(1)求电流
.(1)求电流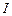 的最小正周期
的最小正周期 和频率
和频率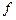 ;(2)设
;(2)设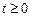 ,求电流
,求电流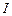 的最大值和最小值,并指出
的最大值和最小值,并指出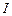 第一次达到最大值和最小值时的
第一次达到最大值和最小值时的 值.
值.
函数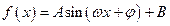
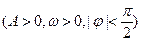 的图像上一个最高点的坐标为
的图像上一个最高点的坐标为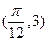 与之相邻的一个最低点的坐标为
与之相邻的一个最低点的坐标为 .
.
(Ⅰ)求 的表达式;
的表达式;
(Ⅱ) 当 ,求函数
,求函数 的单调递增区间和零点.
的单调递增区间和零点.
已知二次函数 的图象过点(0,-3),且
的图象过点(0,-3),且 的解集
的解集 .
.
(Ⅰ)求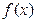 的解析式;
的解析式;
(Ⅱ)求函数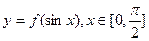 的最值.
的最值.