在矩形ABCD中,|AB|=2 ,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且
,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且 .
.
(Ⅰ)求证:直线ER与GR′的交点P在椭圆 :
: +
+ =1上;
=1上;
(Ⅱ)若M、N为椭圆 上的两点,且直线GM与直线GN的斜率之积为
上的两点,且直线GM与直线GN的斜率之积为 ,求证:直线MN过定点.
,求证:直线MN过定点.
(本小题满分13分)已知函数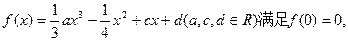
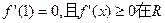 上恒成立.
上恒成立.
(1)求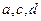 的值;
的值;
(2)若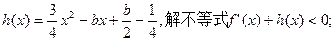
(3)是否存在实数m,使函数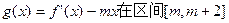 上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
(本小题满分13分)设三次函数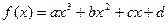
 ,在
,在 处取得极值,其图像在
处取得极值,其图像在 处的切线的斜率为
处的切线的斜率为 。
。
(1)求证: ;
;
(2)若函数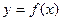 在区间
在区间 上单调递增,求
上单调递增,求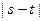 的取值范围。
的取值范围。
本小题满分13分)
已知函数
(1)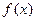 为定义域上的单调函数,求实数
为定义域上的单调函数,求实数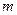 的取值范围
的取值范围
(2)当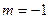 时,求函数
时,求函数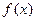 的最大值
的最大值
(3)当 时,且
时,且 ,证明:
,证明: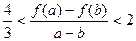
(本小题满分14分,第Ⅰ小题5分,第Ⅱ小题4分,第Ⅲ小题5分).
数列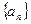 的各项均为正数,
的各项均为正数,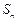 为其前
为其前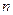 项和,对于任意
项和,对于任意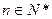 ,总有
,总有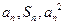 成等差数列.
成等差数列.
(Ⅰ)求数列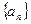 的通项公式;
的通项公式;
(Ⅱ)设数列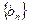 的前
的前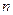 项和为
项和为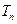 ,且
,且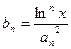 ,求证:对任意实数
,求证:对任意实数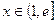 (
( 是常数,
是常数, =2.71828
=2.71828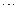 )和任意正整数
)和任意正整数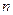 ,总有
,总有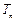
 2;
2;
(Ⅲ) 正数数列 中,
中, .求数列
.求数列 中的最大项.
中的最大项.
(本小题满分14分)
已知数列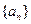 ,
, ,
,
(Ⅰ)求数列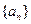 的通项公式
的通项公式
(Ⅱ)当 时,求证:
时,求证: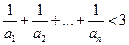
(Ⅲ)若函数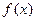 满足:
满足: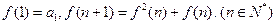
求证: