已知二次函数 的图象经过坐标原点,其导函数为
的图象经过坐标原点,其导函数为 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点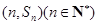 均在函数
均在函数 的图像上.
的图像上.
(1)求 的解析式;
的解析式;
(2)求数列 的通项公式;
的通项公式;
(3)设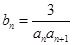 ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数
都成立的最小正整数 .
.
、(本小题满分12分)
已知公差不为零的等差数列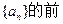 6项和为60,且
6项和为60,且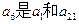 的等比中项。
的等比中项。
(1)求数列 的通项公式;
的通项公式;
(2)若数列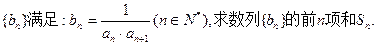
本小题满分12分)
假设一种机器在一个工作日内发生故障的概率为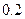 ,若一周5个工作日内无故障,则可获得利润10万元;仅有一个工作日发生故障可获得利润5万元; 仅有两个工作日发生故障不获利也不亏损;有三个或三个以上工作日发生故障就要亏损2万元.求:
,若一周5个工作日内无故障,则可获得利润10万元;仅有一个工作日发生故障可获得利润5万元; 仅有两个工作日发生故障不获利也不亏损;有三个或三个以上工作日发生故障就要亏损2万元.求:
(Ⅰ)一周5个工作日内恰有两个工作日发生故障的概率(保留两位有效数字);
(Ⅱ)一周5个工作日内利润的期望.
(本小题满分12分)已知
(1)求 的值;
的值;
(2)若 为第二象限的角,且
为第二象限的角,且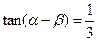 ,求
,求
(本小题满分12分)已知集合 ,若
,若
(1)求实数 的取值范围;
的取值范围;
(2)求 的最值。
的最值。
已知函数

(1)若k=2,求方程 的解;
的解;
(2)若关于x方程 上有两个解
上有两个解 ,求k取值范围并证明
,求k取值范围并证明