如图，已知抛物线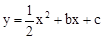（b，c是常数，且c<0）与x轴分别交于点A-优题课

如图，已知抛物线（b，c是常数，且c<0）与x轴分别交于点A，B（点A位于点B的左侧），与y轴的负半轴交于点C，点A的坐标为(－1，0)．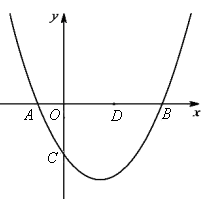

（1）b＝　　，点B的横坐标为　　（上述结果均用含c的代数式表示）；
（2）连接BC，过点A作直线AE∥BC，与抛物线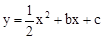交于点E．点D是x轴上一点，其坐标为
(2，0)，当C，D，E三点在同一直线上时，求抛物线的解析式；
（3）在（2）的条件下，点P是x轴下方的抛物线上的一动点，连接PB，PC，设所得△PBC的面积为S．
①求S的取值范围；
②若△PBC的面积S为整数，则这样的△PBC共有　　个．

科目数学题型解答题难度中等

知识点：二次函数在给定区间上的最值

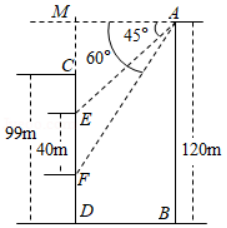
如图，在一座山的前方有一栋住宅，已知山高 $AB = 120 m$ ，楼高 $CD = 99 m$ ，某天上午9时太阳光线从山顶点 $A$ 处照射到住宅的点 $E$ 外．在点 $A$ 处测得点 $E$ 的俯角 $∠ EAM = 45 °$ ，上午10时太阳光线从山顶点 $A$ 处照射到住宅点 $F$ 处，在点 $A$ 处测得点 $F$ 的俯角 $∠ FAM = 60 °$ ，已知每层楼的高度为 $3 m$ ， $EF = 40 m$ ，问：以当天测量数据为依据，不考虑季节天气变化，至少要买该住宅的第几层楼，才能使上午10时太阳光线照射到该层楼的外墙？ $(\sqrt{3} \approx 1.73)$

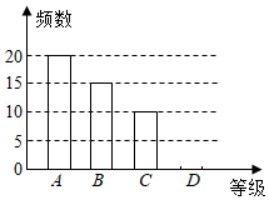
某校开展主题为"防疫常识知多少"的调查活动，抽取了部分学生进行调查，调查问卷设置了 $A$ ：非常了解、 $B$ ：比较了解、 $C$ ：基本了解、 $D$ ：不太了解四个等级，要求每个学生填且只能填其中的一个等级，采取随机抽样的方式，并根据调查结果绘制成如图所示不完整的频数分布表和频数分布直方图，根据以上信息回答下列问题：

等级	频数	频率
$A$	20	0.4
$B$	15	$b$
$C$	10	0.2
$D$	$a$	0.1

（1）频数分布表中 $a =$ 　　， $b =$ 　　，将频数分布直方图补充完整；

（2）若该校有学生1000人，请根据抽样调查结果估算该校"非常了解"和"比较了解"防疫常识的学生共有多少人？

（3）在"非常了解"防疫常识的学生中，某班有5个学生，其中3男2女，计划在这5个学生中随机抽选两个加入防疫志愿者团队，请用列表或画树状图的方法求所选两个学生中至少有一个女生的概率．

如图， $AB$ 交 $CD$ 于点 $O$ ，在 $ΔAOC$ 与 $ΔBOD$ 中，有下列三个条件：① $OC = OD$ ，② $AC = BD$ ，③ $∠ A = ∠ B$ ．请你在上述三个条件中选择两个为条件，另一个能作为这两个条件推出来的结论，并证明你的结论（只要求写出一种正确的选法）．

（1）你选的条件为　　、　　，结论为　　；

（2）证明你的结论．

某品牌汽车销售店销售某种品牌的汽车，每辆汽车的进价16（万元）．当每辆售价为22（万元）时，每月可销售4辆汽车．根据市场行情，现在决定进行降价销售．通过市场调查得到了每辆降价的费用 $y_{1}$ （万元）与月销售量 $x$ （辆 $) (x ⩾ 4)$ 满足某种函数关系的五组对应数据如下表：

$x$	4	5	6	7	8
$y_{1}$	0	0.5	1	1.5	2

（1）请你根据所给材料和初中所学的函数知识写出 $y_{1}$ 与 $x$ 的关系式 $y_{1} =$ 　　；

（2）每辆原售价为22万元，不考虑其它成本，降价后每月销售利润 $y =$ （每辆原售价 $- y_{1} -$ 进价） $x$ ，请你根据上述条件，求出月销售量 $x (x ⩾ 4)$ 为多少时，销售利润最大？最大利润是多少？

如图，抛物线 $y ＝ a x^{2} ﹣ 2 x + c （ a \neq 0 ）$ 与x轴交于 $A 、 B （ 3 ， 0 ）$ 两点，与y轴交于点 $C （ 0 ，﹣ 3 ）$ ，抛物线的顶点为D．

（1）求抛物线的解析式；

（2）点P在抛物线的对称轴上，点Q在x轴上，若以点P、Q、B、C为顶点，BC为边的四边形为平行四边形，请直接写出点P、Q的坐标；

（3）已知点M是x轴上的动点，过点M作x的垂线交抛物线于点G，是否存在这样的点M，使得以点A、M、G为顶点的三角形与 $△ BCD$ 相似，若存在，请求出点M的坐标；若不存在，请说明理由．