已知在平面直角坐标系 中,圆
中,圆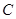 的参数方程为
的参数方程为 (
( 为参数),以
为参数),以 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线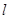 的极坐标方程为
的极坐标方程为 .
.
⑴写出直线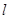 的直角坐标方程和圆
的直角坐标方程和圆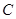 的普通方程;
的普通方程;
⑵求圆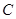 截直线
截直线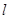 所得的弦长.
所得的弦长.
在直角坐标系中,曲线
的参数方程为 (
为参数).
是曲线
上的动点,点
满足
,
(
为参数).
是曲线
上的动点,点
满足
,
(1)求点 的轨迹方程 ;
(2)在以 为极点, 轴的正半轴为极轴的极坐标系中,射线 与曲线 , 交于不同于原点的点 求 .
如图, 、 分别是 , AC边上的点, , 为方程 的两根()
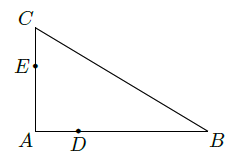
(1)证明
四点共圆
(2)若
,求
四点所在圆的半径
已知函数
,曲线
在点
处的切线方程为
,
(1)求
的值
(2)证明:当
时,
在平面直角坐标系中,曲线
与坐标轴的交点都在圆
上,
(1)求圆
的方程;
(2)如果圆
与直线
交于
两点,且
,求
的值.
某种产品以其质量指标值衡量,质量指标越大越好,且质量指标值大于102的产品为优质产品,现在用两种新配方(
配方、
配方)做试验,各生产了100件,并测量了每件产品的质量指标值,得到下面的试验结果:
配方的频数分布表
| 指标值分组 |
|||||
| 频数 |
8 |
20 |
42 |
22 |
8 |
B配方的频数分布表
| 指标值分组 |
|||||
| 频数 |
4 |
12 |
42 |
32 |
8 |
(1)分别估计使用
配方,B配方生产的产品的优质品的概率;
(2)已知用
配方生产一件产品的利润与其质量指标的关系为:
估计用
配方生产上述产品平均每件的利润。