已知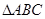 的三内角
的三内角 、
、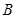 、
、 所对的边分别是
所对的边分别是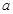 ,
, ,
,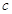 ,向量
,向量 与向量
与向量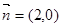 的夹角
的夹角 的余弦值为
的余弦值为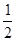
(Ⅰ)求角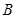 的大小;
的大小;
(Ⅱ)若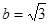 ,求
,求 的范围。
的范围。
已知函数
(I)若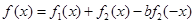 ,是否存在a,b
,是否存在a,b R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
〔II)若a=2,b=1.求函数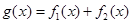 在R上的单调区间;
在R上的单调区间;
(III )对于给定的实数 成立.求a的取值范围.
成立.求a的取值范围.
已知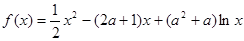 (
( ,
, 是常数),若对曲线
是常数),若对曲线 上任意一点
上任意一点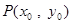 处的切线
处的切线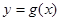 ,
,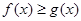 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知函数 ,函数
,函数 是函数
是函数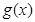 的导函数.
的导函数.
(1)若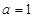 ,求
,求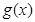 的单调减区间;
的单调减区间;
(2)若对任意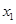 ,
, 且
且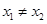 ,都有
,都有 ,求实数
,求实数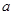 的取值范围;
的取值范围;
(3)在第(2)问求出的实数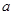 的范围内,若存在一个与
的范围内,若存在一个与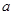 有关的负数
有关的负数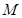 ,使得对任意
,使得对任意 时
时 恒成立,求
恒成立,求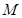 的最小值及相应的
的最小值及相应的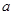 值.
值.
已知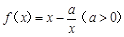 ,
,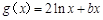 ,且直线
,且直线 与曲线
与曲线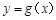 相切.
相切.
(1)若对 内的一切实数
内的一切实数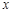 ,不等式
,不等式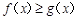 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)当 时,求最大的正整数
时,求最大的正整数 ,使得对
,使得对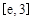 (
( 是自然对数的底数)内的任意
是自然对数的底数)内的任意 个实数
个实数 都有
都有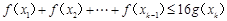 成立;
成立;
(3)求证: .
.
设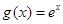 ,
, ,其中
,其中 是常数,且
是常数,且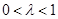 .
.
(1)求函数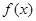 的极值;
的极值;
(2)证明:对任意正数 ,存在正数
,存在正数 ,使不等式
,使不等式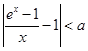 成立;
成立;
(3)设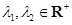 ,且
,且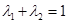 ,证明:对任意正数
,证明:对任意正数 都有:
都有: .
.