设数列 的前
的前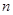 项和
项和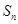 满足
满足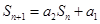 ,其中
,其中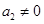 .
.
⑴若 ,求
,求 及
及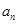 ;
;
⑵若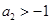 ,求证:
,求证: ,并给出等号成立的充要条件.
,并给出等号成立的充要条件.
(本小题满分14分)
已知函数 .
.
(Ⅰ)求证:存在定点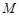 ,使得函数
,使得函数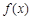 图象上任意一点
图象上任意一点 关于
关于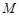 点对称的点
点对称的点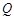 也在函数
也在函数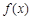 的图象上,并求出点
的图象上,并求出点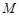 的坐标;
的坐标;
(Ⅱ)定义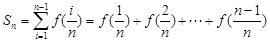 ,其中
,其中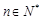 且
且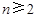 ,求
,求 ;
;
(Ⅲ)对于(Ⅱ)中的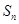 ,求证:对于任意
,求证:对于任意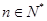 都有
都有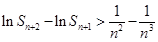 .
.
(本题满分14分)
已知正项数列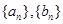 满足:对任意正整数
满足:对任意正整数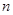 ,都有
,都有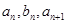 成等差数列,
成等差数列, 成等比数列,且
成等比数列,且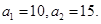
(Ⅰ)求证:数列 是等差数列;
是等差数列;
(Ⅱ)求数列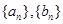 的通项公式;
的通项公式;
(Ⅲ) 设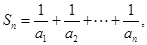 如果对任意正整数
如果对任意正整数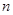 ,不等式
,不等式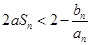 恒成立,求实数
恒成立,求实数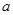 的取值范围.
的取值范围.
(本题满分14分)如图,已知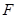 为椭圆
为椭圆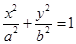
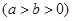 的右焦点,直线
的右焦点,直线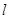 过点
过点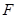 且与双曲线
且与双曲线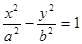 的两条渐进线
的两条渐进线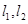 分别交于点
分别交于点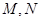 ,与椭圆交于点
,与椭圆交于点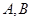 .
.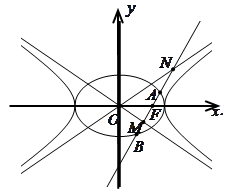
(I)若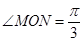 ,双曲线的焦距为4。求椭圆方程。
,双曲线的焦距为4。求椭圆方程。
(II)若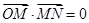 (
(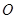 为坐标原点),
为坐标原点),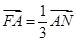 ,求椭圆的离心率
,求椭圆的离心率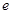
(本题满分14分)如图:多面体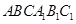 中,三角形
中,三角形 是边长为4的正三角形,
是边长为4的正三角形,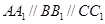 ,
,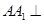 平面
平面 ,
,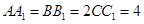 .
.
(1)若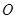 是
是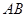 的中点,求证:
的中点,求证: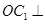
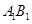 ;
;
(2)求平面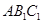 与平面
与平面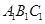 所成的角的余弦值.
所成的角的余弦值.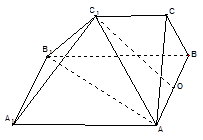
(本小题满分12分)
小白鼠被注射某种药物后,只会表现为以下三种症状中的一种:兴奋、无变化(药物没有发生作用)、迟钝.若出现三种症状的概率依次为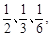 现对三只小白鼠注射这种药物.
现对三只小白鼠注射这种药物.
(Ⅰ)求这三只小白鼠表现症状互不相同的概率;
(Ⅱ)用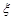 表示三只小白鼠共表现症状的种数,求
表示三只小白鼠共表现症状的种数,求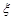 的分布列及数学期望.
的分布列及数学期望.