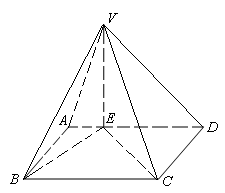
如图,已知四棱锥 ,底面
,底面 是平行四边形,点
是平行四边形,点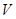 在平面
在平面 上的射影
上的射影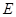 在
在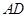 边上,且
边上,且 ,
,
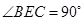 .
.
(Ⅰ)设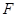 是
是 的中点,求异面直线
的中点,求异面直线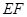 与
与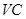 所成角的余弦值;
所成角的余弦值;
(Ⅱ)设点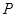 在棱
在棱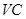 上,且
上,且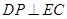 .求
.求 的值.
的值.
设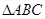 的三个内角
的三个内角 ,
, ,
, 所对的边分别为
所对的边分别为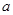 ,
, ,
,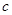 .已知
.已知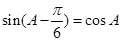 .
.
(1)求角 的大小;
的大小;
(2)若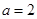 ,求
,求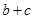 的最大值.
的最大值.
某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有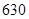 名学生,男女生人数之比为
名学生,男女生人数之比为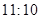 ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为 .
.
(1)求抽取的男学生人数和女学生人数;
(2)通过对被抽取的学生的问卷调查,得到如下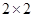 列联表:
列联表:
| 否定 |
肯定 |
总计 |
|
| 男生 |
10 |
||
| 女生 |
30 |
||
| 总计 |
①完成列联表;
②能否有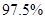 的把握认为态度与性别有关?
的把握认为态度与性别有关?
(3)若一班有 名男生被抽到,其中
名男生被抽到,其中 人持否定态度,
人持否定态度,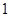 人持肯定态度;二班有
人持肯定态度;二班有 名女生被抽到,其中
名女生被抽到,其中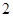 人持否定态度,
人持否定态度,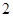 人持肯定态度.
人持肯定态度.
现从这 人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
解答时可参考下面临界值表:
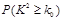 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
已知椭圆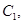
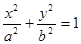 (a>b>0)抛物线
(a>b>0)抛物线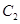
 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
 |
 |
4 |
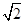 |
1 |
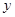 |
2 |
4 |
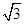 |
2 |
(1)求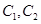 的标准方程;
的标准方程;
(2)四边形ABCD的顶点在椭圆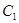 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若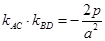 ,
,
(i) 求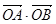 的最值.
的最值.
(ii) 求四边形ABCD的面积;
已知各项均不相等的等差数列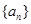 的前三项和为18,
的前三项和为18, 是一个与
是一个与 无关的常数,若
无关的常数,若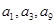 恰为等比数列
恰为等比数列 的前三项,
的前三项,
(1)求 的通项公式.
的通项公式.
(2)记数列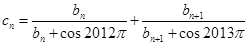 ,
,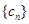 的前三
的前三 项和为
项和为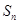 ,求证:
,求证: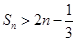
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。将△ABD沿边AB折起, 使得△ABD与△ABC成30o的二面角 ,如图二,在二面角
,如图二,在二面角 中.
中.
(1) 求CD与面ABC所成的角正弦值的大小;
(2) 对于AD上任意点H,CH是否与面ABD垂直。