在ΔABC中,内角A、B、C的对边分别为a、b、c,已知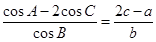
(1)求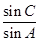 的值;(2)若
的值;(2)若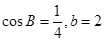 ,求ΔABC的面积。
,求ΔABC的面积。
在平面直角坐标系xoy中,点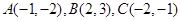 。
。
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足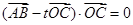 ,求t的值。
,求t的值。
设函数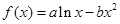 .
.
(1)若函数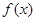 在
在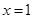 处与直线
处与直线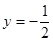 相切,
相切,
①求实数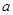 ,
, 的值;
的值;
②求函数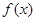 在
在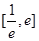 上的最大值;
上的最大值;
(2)当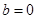 时,若不等式
时,若不等式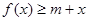 对所有的
对所有的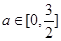 ,
,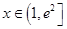 都成立,求实数
都成立,求实数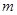 的取值范围.
的取值范围.
设椭圆 的右焦点为
的右焦点为 ,直线
,直线 与
与 轴交于点
轴交于点 ,若
,若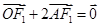 (其中
(其中 为坐标原点).
为坐标原点).
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设 是椭圆
是椭圆 上的任一点,
上的任一点,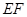 为圆
为圆 的任一条直径,求
的任一条直径,求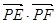 的最大值.
的最大值.
已知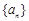 是正数组成的数列,
是正数组成的数列, ,且点
,且点
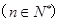 在函数
在函数 的图象上.
的图象上.
(1)求数列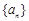 的通项公式;
的通项公式;
(2)若列数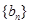 满足
满足 ,
,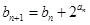 ,求证:
,求证: